Đề thi giữa HK2 môn Toán 10 CTST năm 2023-2024
Trường THPT Nguyễn Văn Linh
-
Câu 1:
Điều kiện để tam thức bậc hai ax2+bx+c(a≠0)ax2+bx+c(a≠0) nhận giá trị âm với mọi x∈R là?
A. Δ>0
B. Δ<0
C. Δ<0 và a>0
D. Δ<0 và a<0
-
Câu 2:
Bảng xét dấu sau đây là của tam thức bậc hai nào?
A. x2−x+6
B. x2+x+6
C. x2−x−6
D. −x2+x−6
-
Câu 3:
Nghiệm của bất phương trình x2−8x+15≤0 là?
A. x∈[3;5]
B. x∈(3;5)
C. x∈(−∞;3]∪[5;+∞)
D. x∈(−∞;3)∪(5;+∞)
-
Câu 4:
Với giá trị nào của m thì bất phương trình −x2−x+m≥0 vô nghiệm?
A. m≥−14
B. m>−14
C. m≤−14
D. m<−14
-
Câu 5:
Một đường hầm xuyên thẳng qua núi và có mặt cắt là một parabol (thông số như hình bên). Giả sử một chiếc xe tải có chiều ngang 6m đi vào vị trí chính giữa miệng hầm. Hỏi chiều cao h của xe tải cần thoả mãn điều kiện gì để có thể đi vào cửa hầm mà không chạm tường?
A. 0<h<6
B. 0<h≤6
C. 0<h<7
D. 0<h≤7
-
Câu 6:
Giá trị nào của m thì phương trình (m−3)x2+(m+3)x−(m+1)=0 có hai nghiệm phân biệt?
A. m∈(−∞;−35)∪(1;+∞)∖{3}
B. m∈(−35;1)
C. m∈(−35;+∞)
D. m∈R∖{3}
-
Câu 7:
Tìm các giá trị của tham số m để bất phương trình −x2+(2m−1)x+m<0 có tập nghiệm là R?
A. m=12
B. m=−12
C. m∈R
D. Không tồn tại m
-
Câu 8:
Với giá trị nào của m thì bất phương trình x2−x+m≤0 vô nghiệm?
A. m<1
B. m>1
C. m<14
D. m>14
-
Câu 9:
Bất phương trình x2−(m+2)x+m+2≤0 vô nghiệm khi và chỉ khi?
A. m∈(−∞;−2]∪[2;+∞)
B. m∈(−∞;−2)∪(2;+∞)
C. m∈(−2;2)
D. m∈[−2;2]
-
Câu 10:
Xác định m để với mọi x, ta có −1≤x2+5x+m2x2−3x+2<7?
A. −53≤m<1
B. 1<m≤53
C. m≤−53
D. m<1
-
Câu 11:
Xác định m để (x−1)[x2+2(m+3)x+4m+12]=0 có ba nghiệm phân biệt lớn hơn −1?
A. m<−72
B. −72<m<−3 và m≠−196
C. −2<m<1 và m≠−169
D. −72<m<−1 và m≠−169
-
Câu 12:
Tam thức bậc hai f(x)=x2+(√5−1)x−√5 nhận giá trị dương khi?
A. x∈(−√5;1)
B. x∈(−∞;−√5)∪(1;+∞)
C. x∈(−√5;+∞)
D. x∈(−∞;1)
-
Câu 13:
Cho phương trình √x4−3x2+2=x2+2. Nếu đặt t=x2,t≥0 thì phương trình đã cho trở thành phương trình nào sau đây?
A. √t2−3t+2=t2+2
B. √t2−3t+2=t+2
C. √t2−3t+2=t−2
D. √t2+3t−2=t+2
-
Câu 14:
Số nghiệm của phương trình √x2−4|x|+3=2x−1 là?
A. 1
B. 2
C. 4
D. 0
-
Câu 15:
Tập nghiệm của phương trình √x2−4x+3=x+1 là?
A. S=∅
B. S={13}
C. S={3}
D. S={1}
-
Câu 16:
Số nghiệm của phương trình √x2−3x+2=√2x2−7|x|+4 là?
A. 1
B. 2
C. 3
D. 4
-
Câu 17:
Tập nghiệm của phương trình √3x2−6x−4=√x−8 là?
A. S={34;1}
B. S={34}
C. S={1}
D. S=∅
-
Câu 18:
Phương trình 2x2−6x+4=3√x3+8 có hai nghiệm dạng x=a±b√13 với a,b∈N. Tính a2−b?
A. 0
B. 1
C. 8
D. -1
-
Câu 19:
Trong mặt phẳng toạ độ Oxy cho các vectơ →a,→b,→c,→d được vẽ ở hình bên. Ta có các khẳng định sau:
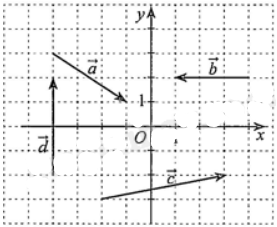
A) →a=(2;−3); B) →b=(−3;0); C) →c=(5;1); D) →d=(4;0).
Số khẳng định đúng là?
A. 0
B. 1
C. 2
D. 3
-
Câu 20:
Trong mặt phẳng toạ độ Oxy, cho →a=(2;−3),→b=(−2;5). Toạ độ của vectơ −→a+3→b là?
A. (8;18)
B. (−8;−18)
C. (−8;18)
D. (8;−18)
-
Câu 21:
Trong mặt phẳng toạ độ Oxy, cho →a=(1;2),→b=(3;−3). Toạ độ của vectơ →c=3→a−2→b là?
A. (−3;12)
B. (3;12)
C. (9;0)
D. (−3;0)
-
Câu 22:
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(5;4),B(−1;0). Đường trung trực của đoạn thẳng AB có phương trình là?
A. x−2y+5=0
B. 3x+2y−10=0
C. 3x+2y−5=0
D. 2x+3y−1=0
-
Câu 23:
Trong mặt phẳng tọ̣ độ Oxy, cho ba điểm A(2;4),B(0;−2),C(5;3). Đường thẳng đi qua điểm A và song song với đường thẳng BC có phương trình là?
A. x−y+5=0
B. x+y−5=0
C. x−y+2=0
D. x+y=0
-
Câu 24:
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(5;2),B(5;−2),C(4;−3). Đường thẳng đi qua điểm A và vuông góc với đường thẳng BC có phương trình là?
A. x−y+7=0
B. x+y−7=0
C. x−y−5=0
D. x+y=0
-
Câu 25:
Phương trình tổng quát của đường thẳng đi qua điểm A(1;−3) và có vectơ pháp tuyến →n(2;−1) là?
A. 2x+y−5=0
B. 2x−y−5=0
C. x+2y+5=0
D. x+2y−5=0
-
Câu 26:
Phương trình tham số của đường thẳng đi qua điểm M(2;1) và có vectơ chỉ phương →u(−1;4) là?
A. {x=2+ty=1−4t
B. {x=−1+2ty=4+t
C. {x=1+4ty=2−t
D. {x=2−ty=1+4t
-
Câu 27:
Phương trình đường thẳng đi qua hai điểm M(−1;0),N(3;1) là?
A. x−4y+1=0
B. x−4y−1=0
C. 4x+y+4=0
D. 4x+y−4=0
-
Câu 28:
Trong mặt phẳng toạ độ, cho đường thẳng d: {x=−1−2ty=4+3t. Vectơ chỉ phương của đường thẳng d là?
A. →u=(−1;4)
B. →u=(−2;3)
C. →u=(3;−2)
D. →u=(2;3)
-
Câu 29:
Trong mặt phẳng toạ độ Oxy, cho điểm M(2;4) và đường thẳng Δ:{x=5+3ty=−5−4t. Khoảng cách từ M đến đường thẳng Δ là?
A. 52
B. 3
C. 5
D. 95
-
Câu 30:
Cho hai đường thẳng d1:3x−4y+5=0,d2:4x−3y+2=0. Điểm M nào sau đây cách đều hai đường thẳng trên?
A. M(1;0)
B. M(2;3)
C. M(4;−2)
D. M(−1;2)
-
Câu 31:
Trong mặt phẳng toạ độ, cho đường thẳng Δ:x−2y−3=0. Đường thẳng nào sau đây có vị trí tương đối trùng với đường thẳng Δ?
A. Δ1:x+2y−3=0
B. Δ2:2x+y−3=0
C. Δ3:2x−4y−1=0
D. Δ4:2x−4y−6=0
-
Câu 32:
Góc giữa hai đường thẳng Δ1:{x=2+ty=−1+√3t và Δ2:{x=3−√3ty=5−t là?
A. 300
B. 450
C. 600
D. 900
-
Câu 33:
Đường tròn nào sau đây có tâm là I(−3;5) và có bán kính là R=4?
A. x2+y2−3x+5y+9=0
B. x2+y2−3x+5y−9=0
C. x2+y2+6x−10y−18=0
D. x2+y2+6x−10y+18=0
-
Câu 34:
Phương trình đường tròn có tâm I(1;2) và đi qua điểm A(−1;3) là?
A. (x+1)2+(y+2)2=25
B. (x+1)2+(y+2)2=5
C. (x−1)2+(y−2)2=5
D. (x−1)2+(y−2)2=25
-
Câu 35:
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(−4;6) và B(−2;4). Phương trình đường tròn có đường kính AB là?
A. (x+3)2+(y−5)2=2
B. (x+3)2+(y+5)2=2
C. (x−3)2+(y+5)2=2√2
D. (x−3)2+(y−5)2=2√2
-
Câu 36:
Một vật chuyển động có vận tốc (mét/giây) được biểu diễn theo thời gian t (giây) bằng công thức v(t)=12t2−4t+10. Hỏi sau tối thiểu bao nhiêu giây thì vận tốc của vật không bé hơn 10m/s (biết rằng t>0)?
A. 10 giây
B. 0 giây
C. 9 giây
D. 8 giây
-
Câu 37:
Giải phương trình sau: √2x2+5=√x2−x+11?
A. S={2;−3}
B. S=2
C. S=−3
D. Vô nghiệm
-
Câu 38:
Cho các vectơ →a=(1;−2),→b=(−2;−6),→c=(m+n;−m−4n). Tìm góc tạo bởi hai vectơ →a,→b?
A. 90∘
B. 45∘
C. 30∘
D. 60∘
-
Câu 39:
Có ba ngôi làng A,B,C mỗi làng cách nhau 6km (ba ngôi làng không cùng nằm trên một đường thẳng). Vào lúc 6 giờ sáng, một người chạy từ A đến B với vận tốc 10km/h và cùng lúc đó một người đạp xe từ C đến B với vận tốc 12km/h. Thời điểm sớm nhất mà hai người cách nhau 1km (theo đường chim bay) là?
A. 6 giờ 25 phút
B. 6 giờ 30 phút
C. 7 giờ kém 25 phút
D. 6 giờ 50 phút
-
Câu 40:
Fahrenheit là một thang đo nhiệt độ nhiệt động lực học, với điểm đóng băng của nước là 32 độ F(0F) và điểm sôi là 2120F (ở áp suất khí quyển tiêu chuẩn). Việc quy đổi nhiệt độ giữa đơn vị độ C và đơn vị độ F được xác định bởi hai điểm trên mặt phẳng toạ độ: Điểm đóng băng của nước là (0;32) và Điểm sôi của (Kết quả làm tròn đến chữ số hàng phần trăm)?
A. 23,560C
B. 122,40C
C. 37,780C
D. 2120C



.PNG)
.PNG)
.PNG)











