Đề thi giữa HK1 môn Toán 9 năm 2022-2023
Trường THCS Lương Thế Vinh
-
Câu 1:
Tìm điều kiện xác định của \(\sqrt {5 - 3x} \)
A. \(x \le \frac{5}{3}\)
B. \(x \ge \frac{5}{3}\)
C. \(x \ge \frac{3}{5}\)
D. \(x \le \frac{3}{5}\)
-
Câu 2:
Tìm x để \(\sqrt {\frac{{ - 2}}{{3x - 1}}} \) có nghĩa
A. \(x < \frac{1}{3}\)
B. \(x \le \frac{1}{3}\)
C. \(x \ge \frac{1}{3}\)
D. \(x > \frac{1}{3}\)
-
Câu 3:
Rút ngọn biểu thức: A = \(\sqrt {144{a^2}} - 9a\) với a > 0
A. - 9a
B. - 3a
C. 3a
D. 9a
-
Câu 4:
Tính giá trị biểu thức : \(9\sqrt {{{\left( { - \frac{8}{3}} \right)}^2}} + \sqrt {{{\left( { - 0,8} \right)}^2}} \)
A. 24,64
B. 32
C. - 24,8
D. 24,8
-
Câu 5:
Biểu thức \(\mathrm{B}=\frac{2}{\sqrt{1-3 x}}\) xác định khi
A. \(x<\frac{1}{3}\)
B. \(x>\frac{1}{3}\)
C. \(x\le\frac{1}{3}\)
D. \(x\ge\frac{1}{3}\)
-
Câu 6:
Thu gọn \(A=\sqrt{11+6 \sqrt{2}}\) ta được
A. \(3+\sqrt{2}\)
B. \(3-\sqrt{2}\)
C. \(-3+\sqrt{2}\)
D. 0
-
Câu 7:
Giá trị của \(E=\sqrt{(\sqrt{3}+1)^{2}}\) là
A. \(\sqrt{3}-1\)
B. \(\sqrt{3}+1\)
C. \(-\sqrt{3}-1\)
D. \(1-\sqrt{3}\)
-
Câu 8:
Biểu thức \(D=\sqrt{-x^{2}+7 x-12}\) xác định khi
A. \( x \leq 4\)
B. \(-3 \leq x \leq 4\)
C. \(x\ge 3\)
D. \(3 \leq x \leq 4\)
-
Câu 9:
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BH = 8cm, tính diện tích tam giác ABC.
A. 36 cm2
B. \(36\sqrt 5 c{m^2}\)
C. 38 cm2
D. \(38\sqrt 5 c{m^2}\)
-
Câu 10:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài các đoạn thẳng CH
A. CH = 96
B. CH = 49
C. CH = 98
D. CH = 89
-
Câu 11:
Cho tam giác ABC vuông tại A có đường cao AH, cho BH = 17cm, HC = 11cm. Độ dài của AH gần đúng với kết quả nào sau đây?
A. 15,4cm
B. 16cm
C. 19,6cm
D. 13,7cm
-
Câu 12:
Cho tam giác ABC vuông tại A có đường cao AH, cho AC = 13cm, BC = 25cm. Độ dài của CH gần đúng với kết quả nào sau đây?
A. 6,8cm
B. 11,5cm
C. 12,7cm
D. 21,3cm
-
Câu 13:
Giá trị của biểu thức \(A = \sqrt {9 - 2\sqrt {14} } + \sqrt {9 + 2\sqrt {14} } \) là?
A. \(2\sqrt 2 \)
B. \(2\sqrt 7 \)
C. \(\sqrt {14} \)
D. 2
-
Câu 14:
Kết quả rút gọn của biểu thức \(\frac{{a + \sqrt {ab} }}{{b + \sqrt {ab} }}\) (với a, b > 0) là ?
A. \(\frac{a}{b}\)
B. \(\frac{a}{{\sqrt b }}\)
C. \(\sqrt {\frac{a}{b}} \)
D. \(\frac{{\sqrt a }}{b}\)
-
Câu 15:
Tính \(\sqrt {5,{5^2}{\rm{ }} - {\rm{ }}3,{5^2}{\rm{ }}} \)
A. 3
B. \(2\sqrt3\)
C. \(3\sqrt2\)
D. 2
-
Câu 16:
Giá trị biểu thức \(\sqrt {5x + 3} .\sqrt {5x - 3} \) khi \(x = \sqrt {3,6} \) là?
A. 3,6
B. 3
C. 81
D. 9
-
Câu 17:
Rút gọn biểu thức sau \( T = (1 + cos\alpha )(1 - cos\alpha ) - ta{n^2}\alpha + si{n^2}\alpha .ta{n^2}\alpha \)
A. 1
B. sinα
C. cosα
D. 0
-
Câu 18:
Cho tam giác ABC vuông tại A. Biết AB = 5, BC = 10. Giá trị của sinB và cosB lần lượt là
A. \( sinB = \frac{1}{2};cosB = \frac{{\sqrt 3 }}{2}\)
B. \( sinB = \frac{{\sqrt 3 }}{2};cosB = \frac{1}{2}\)
C. \( sinB = \frac{1}{{\sqrt 2 }};cosB = \frac{{\sqrt 3 }}{2}\)
D. \( sinB = \frac{{\sqrt 3 }}{2};cosB = \frac{1}{{\sqrt 2 }}\)
-
Câu 19:
Phương trình để từ đó có thể tìm được x (không phải giải phương trình này:
A. \(sin30^∘=x.sin80^∘\)
B. \( x.sin30^∘=sin80^∘\)
C. \((1-x)sin30^∘=4.sin80^∘\)
D. \( x.sin30^∘=4.sin80^∘\)
-
Câu 20:
Thang AB dài 6,7m tựa vào tường làm thành góc 630 với mặt đất. Hỏi chiều cao của thang đạt được so với mặt đất ?
A. 5m
B. 4m
C. 6m
D. 7m
-
Câu 21:
Tính \(a{b^2}\sqrt {\frac{3}{{{a^2}{b^4}}}} \left( {a < 0} \right)\)
A. \(\sqrt3\)
B. \(-\sqrt3\)
C. \(2\sqrt3\)
D. \(-2\sqrt3\)
-
Câu 22:
Tính \(B{\rm{ }} = {\rm{ }}\sqrt {4{\rm{ }} + {\rm{ }}\sqrt 7 } {\rm{ }} + {\rm{ }}\sqrt {4{\rm{ }} - {\rm{ }}\sqrt 7 } \)
A. \(B = 2\sqrt 7 -2\)
B. \(B = 2\sqrt 7+2\)
C. \(B = 2\sqrt 7 \)
D. \(B = \sqrt {14}\)
-
Câu 23:
Giá trị của \(\frac{{\sqrt {80} }}{{\sqrt 5 }}\) bằng:
A. 16
B. \(4\sqrt5\)
C. \(\sqrt4\)
D. 4
-
Câu 24:
Tính \(\frac{{\sqrt 8 }}{{\sqrt 2 }} + \frac{{\sqrt {27} }}{{\sqrt 3 }} + \frac{{\sqrt {80} }}{{\sqrt 5 }}\)
A. 9
B. -9
C. 9,17
D. -9,17
-
Câu 25:
Biểu thức \(P = \sqrt 5 \left( {\sqrt {10} - \sqrt {40} } \right)\) có giá trị bằng:
A. \( - 5\sqrt {10}\)
B. \( - 5\sqrt 6\)
C. \(- 5\sqrt {30}\)
D. \( - 5\sqrt 2\)
-
Câu 26:
Rút gọn biểu thức \(P = \frac{{\sqrt {16} + \sqrt {36} }}{{2\sqrt {25} }}\) ta được:
A. P = 1
B. P = 2
C. P = 4
D. P = 3
-
Câu 27:
Rút gọn biểu thức \(\sqrt {7 - 4\sqrt 3 } + \sqrt 3 \) ta được kết quả là
A. 2
B. \(2\sqrt 3 - 2\)
C. \(2\sqrt 3 + 2\)
D. \(2 - \sqrt 3\)
-
Câu 28:
Trục căn thức ở mẫu của \(\frac{2}{\sqrt{3}+1}\) ta được
A. \(1-\sqrt{3}\)
B. \(\sqrt{3}-1\)
C. \(\sqrt{3}+1\)
D. \(-\sqrt{3}-1\)
-
Câu 29:
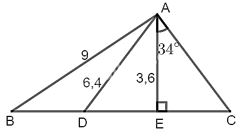
Cho hình:
Biết: \( AB = 9cm,AC = 6,4cm;AN = 3,6cm,\widehat {AN{\rm{D}}} = {90^ \circ },\widehat {DAN} = {34^ \circ }\). Tính CN
A. 5,2cm
B. 6cm
C. 4,2cm
D. 7cm
-
Câu 30:
Để vẽ một tam giác cân có góc ở đáy là 500 mà không có thước đo góc, một học sinh vẽ một tam giác cân có cạnh bên 3cm, cạnh đáy 4cm. Tính góc ở đáy mà em học sinh đó đã vẽ.
A. \({50^ \circ }{11^\prime }\)
B. \({48^ \circ }{11^\prime }\)
C. \({49^ \circ }{11^\prime }\)
D. \({51^ \circ }{11^\prime }\)
-
Câu 31:
Rút gọn biểu thức: \( A = \frac{{3 + \sqrt 5 }}{{\sqrt 5 + 2}} + \frac{{\sqrt 5 }}{{\sqrt 5 - 1}} - \frac{{3\sqrt 5 }}{{3 + \sqrt 5 }}.\)
A. \( A = 4 - \sqrt 5 \)
B. \( A = -4 - \sqrt 5 \)
C. \( A = 4 + \sqrt 5 \)
D. \( A = -4 + \sqrt 5 \)
-
Câu 32:
Tính: \( C = \frac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 \)
A. 0
B. -1
C. 1
D. 2
-
Câu 33:
Tính: \( B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} \)
A. 5
B. 7
C. 6
D. 8
-
Câu 34:
Giá trị x để \(A=\frac{2+5 \sqrt{x}}{\sqrt{x}+3}\) có giá trị bằng \(\frac{1}{2}\) là
A. \(x=\frac{1}{121}\)
B. \(x=\frac{1}{11}\)
C. \(x=\frac{1}{15}\)
D. \(x=\frac{1}{13}\)
-
Câu 35:
Cho tam giác ABC vuông tại A. Tính \( A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\:\)
A. 0
B. 1
C. 2
D. 3
-
Câu 36:
Một con mèo ở trên cành cây cao 6,5m. Để bắt mèo xuống cần phải đặt thang sao cho đầu thang đạt độ cao đó, khi đó góc của thang với mặt đất là bao nhiêu, biết chiếc thang dài 6,7m ?
A. \( {75^ \circ }{57^\prime }\)
B. \( {65^ \circ }{57^\prime }\)
C. \( {55^ \circ }{57^\prime }\)
D. \( {45^ \circ }{57^\prime }\)
-
Câu 37:
Sau khi trục căn thức ở mẫu của biểu thức \( \frac{3}{{\sqrt[3]{4} + 1}}\)
A. \(\sqrt[3]{{16}} - \sqrt[3]{4} - 1\)
B. \( \sqrt[3]{{16}} + \sqrt[3]{4} - 1\)
C. \( \sqrt[3]{{16}} - \sqrt[3]{4}+ 1\)
D. \( \sqrt[3]{{16}} + \sqrt[3]{4} + 1\)
-
Câu 38:
Rút gọn các biểu thức: \( \left( {15\sqrt {200} - 3\sqrt {450} + 2\sqrt {50} } \right):\sqrt {10} .\)
A. \(23\sqrt5\)
B. \(\sqrt5\)
C. \(23\sqrt2\)
D. \(\sqrt2\)
-
Câu 39:
So sánh hai số \(5\sqrt3\) và \(4\sqrt5\)
A. \( 5\sqrt 3 > 4\sqrt 5 \)
B. \( 5\sqrt 3 = 4\sqrt 5 \)
C. \( 5\sqrt 3 \ge 4\sqrt 5 \)
D. \( 5\sqrt 3 < 4\sqrt 5 \)
-
Câu 40:
Đưa thừa số \( \sqrt {144{{\left( {3 + 2a} \right)}^4}} \) ra ngoài dấu căn ta được?
A. \( 12{\left( {3 + 2a} \right)^4}\)
B. \( 144{\left( {3 + 2a} \right)^2}\)
C. \(-12{\left( {3 + 2a} \right)^2}\)
D. \( 12{\left( {3 + 2a} \right)^2}\)



.JPG)
.JPG)