Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài các đoạn thẳng CH
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai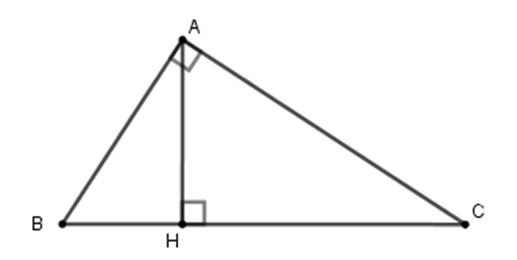
Ta có: AB : AC = 3 : 7, đặt AB = 3a; AC = 7a (a > 0)
Theo hệ thức lượng:
\(\begin{array}{*{20}{l}}
{\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Rightarrow \frac{1}{{42}} = \frac{1}{{9{a^2}}} + \frac{1}{{{{49}^2}}} \Rightarrow \frac{1}{{1764}} = \frac{{58}}{{441{a^2}}}}\\
{ \Rightarrow 441{a^2} = 102312 \Rightarrow A = 2\sqrt {58} (TM) \Rightarrow AB = 6\sqrt {58} ;AC = 14\sqrt {58} }
\end{array}\)
Theo định lý Py-ta-go cho tam giác vuông AHC ta có:
\(CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {{{(14\sqrt {58} )}^2} - {{42}^2}} = 98\)
Vậy CH = 98
Đề thi giữa HK1 môn Toán 9 năm 2022-2023
Trường THCS Lương Thế Vinh



.JPG)
.JPG)











