10 Đề thi kiểm tra cuối HK1 môn Toán lớp 9 - KNTT - Đề 2
22 câu hỏi 60 phút
Không giải hệ phương trình, dự đoán số nghiệm của hệ \(\left\{\begin{array}{l}-x+5 y=-1 \\ 5 x+y=2\end{array}\right.\)
Vô số nghiệm
Vô nghiệm
Có nghiệm duy nhất
Có hai nghiệm phân biệt
Vì \(\frac {-1}{5} \neq \frac {5}{1}\)
Danh sách câu hỏi:
Vì \(\frac {-1}{5} \neq \frac {5}{1}\)
Gọi số vở mỗi loại mà Lan có thể mua nhiều nhất là \(x\left(x \in \mathbb{N}^*\right)\).
Như vậy tổng số tiền mua \(x\) quyển giá 7500 đồng và \(x\) quyển giá 6000 nhỏ hơn hoặc bằng 85000 đồng hay \(7500 x+6000 x \leq 85000\).
Xét tam giác ABC vuông tại A có: \(\mathrm{b}=a \cdot \sin \mathrm{~B}=a \cdot \cos C\)
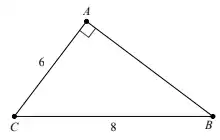
Theo định lý Pytago ta có: \(B C^2=A C^2+A B^2 \Rightarrow A B=\sqrt{8^2-6^2} \approx 5,29\).
Xét tam giác \(A B C\) vuông tại \(C\) có \(\tan C=\frac{A B}{A C} \approx \frac{5,29}{6} \approx 0,88\).
Câu 5:
Cho hình vuông ABCD, O là tâm của đường tròn nội tiếp hình vuông. Khẳng định nào sau đây đúng?
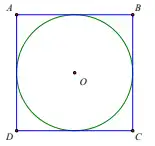
O là tâm của đường tròn nội tiếp hình vuông ABCD.
Do đó (O) tiếp xúc với các cạnh của hình vuông
Hay AB, BC, CD, DA đều là tiếp tuyến của đường tròn (O).
Câu 13:
Cho phương trình \(x^3-x^2+4 x-4=0\), khi đó
Nghiệm của phương trình là \(x=1 ; x=2\)
Nghiệm của phương trình là có một nghiệm nguyên
Nghiệm của phương trình là \(x=1\)
Nghiệm của phương trình là \(x=2\)
Câu 14:
Các mệnh đề sau đúng hay sai?
Gọi \(d\) là khoảng cách hai tâm của hai đường tròn \((O, R)\) và \(\left(O^{\prime} ; r\right)\) (với \(0<r<R\) ). Để \((\mathrm{O} ; \mathrm{R})\) và \(\left(\mathrm{O}^{\prime} ; \mathrm{r}\right)\) đựng nhau thì \(\mathrm{d}<\mathrm{R}-\mathrm{r}\)
Cho đoạn thẳng \(\mathrm{OO}^{\prime}=10 \mathrm{~cm}\). Vẽ các đường tròn \((\mathrm{O} ; 6 \mathrm{~cm})\) và \(\left(\mathrm{O}^{\prime} ; 4 \mathrm{~cm}\right)\). Hai đường tròn \((\mathrm{O}) ;\left(\mathrm{O}^{\prime}\right)\) tiếp xúc ngoài nhau
Cho \((\mathrm{O}, 15 \mathrm{~cm})\) dây AB của đường tròn cách tâm O một khoảng là 9 cm. Khi đó dây \(\mathrm{AB}=12 \mathrm{~cm}\)
Cho \((\mathrm{O} ; 7 \mathrm{~cm})\) và đường thẳng d. Gọi OH là khoảng cách từ tâm O đến đường thẳng d. Điều kiện để d và \((\mathrm{O})\) có điểm chung là \(\mathrm{OH}=7 \mathrm{~cm}\)
Câu 15:
Cho biểu thức \(P=\frac{45}{10-5 \sqrt{3}}\)
Kết quả trục căn thức ở mẫu của biểu thức \(P\) là \(18+9 \sqrt{3}\)
\(P\) có dạng \(a+b \sqrt{3}\). Tích \(a . b\) là 2
Nghiệm của phương trình \(x^2-(P-9 \sqrt{3}) x=0\) là 18
Kết quả so sánh biểu thức \(P\) với 34 là \(P<34\)
Câu 16:
Cho phương trình \(\sqrt{x+4-2 \sqrt{x+3}}=2\)
Phương trình xác định với mọi giá trị của \(x\)
ĐKXĐ: \(x \leq-3\)
ĐKXĐ: \(x \geq-3\)
ĐKXĐ: \(x \geq-4\)
