500 câu trắc nghiệm cuối HK1 Toán 9 - KNTT - Đề 2
22 câu hỏi 60 phút
Một số tự nhiên có hai chữ số, tổng của chữ số hàng chục và chữ số hàng đơn vị là 9, biết chữ số hàng chục gấp 2 lần chữ số hàng đơn vị. Số cần tìm là
42
45
63
84
Gọi chữ số hàng chục là \(x ; x \in \mathbb{N} ; 0<x \leq 9\);
chữ số hàng đơn vị là \(y ; y \in \mathbb{N} ; y \leq 4\).
Theo đề bài ta có hệ phương trình:
\(\left\{\begin{array}{l}x+y=9 \\x=2 y\end{array} \\\left\{\begin{array}{l}2 y+y=9 \\x=2 y\end{array} \\\left\{\begin{array}{l}3 y=9 \\x=2 y\end{array}\\\left\{\begin{array}{l}y=3 \\x=6\end{array}\right.\right.\right.\right.\)
Vậy số cần tìm là 63.
Danh sách câu hỏi:
Gọi chữ số hàng chục là \(x ; x \in \mathbb{N} ; 0<x \leq 9\);
chữ số hàng đơn vị là \(y ; y \in \mathbb{N} ; y \leq 4\).
Theo đề bài ta có hệ phương trình:
\(\left\{\begin{array}{l}x+y=9 \\x=2 y\end{array} \\\left\{\begin{array}{l}2 y+y=9 \\x=2 y\end{array} \\\left\{\begin{array}{l}3 y=9 \\x=2 y\end{array}\\\left\{\begin{array}{l}y=3 \\x=6\end{array}\right.\right.\right.\right.\)
Vậy số cần tìm là 63.
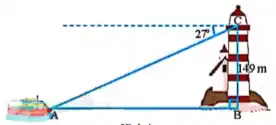
Xét \(\triangle A B C\) vuông tại B, có: \(A B=B C .\cot \widehat{B A C}=149 . \cot 27^{\circ} \approx 292~(\mathrm{m})\) Khoảng cách từ du thuyền đến chân ngọn hải đăng khoảng \(292\text{ m}\).
Xét \(\triangle A B C\) vuông tại \(A\) có
\(\begin{aligned}& \tan C=\frac{A B}{A C} \Rightarrow A B=A C \cdot \tan C=20 \cdot \tan 60^{\circ}=20 \sqrt{3} \\& \cos C=\frac{A C}{B C} \Rightarrow B C=\frac{A C}{\cos C}=\frac{20}{\cos 60^{\circ}}=40\end{aligned}\)
Vậy \(A B=20 \sqrt{3} ; B C=40\)
Biểu thức \(\sqrt{3 x-1}\) có nghĩa khi \(3 x-1 \geq 0 \Rightarrow 3 x \geq 1 \Rightarrow x \geq \frac{1}{3}\)
Ta có \(\sqrt[3]{125 a^3}=\sqrt[3]{(5 a)^3}=5 a\)
Câu 7:
Công thức tính độ dài \(l\) của cung \(n^{\circ}\) trên đường tròn (\(\mathrm{O} ; \mathrm{R}\)) là:
Câu 11:
Trong các hệ phương trình dưới đây, hệ phương trình nào là hệ hai phương trình bậc nhất hai ẩn?
Câu 13:
Cho biểu thức \(\sqrt{(2-x)^2}\)
Với \({x}>2\) khi rút gọn biểu thức ta được kết quả là \(-{x}-2\)
Giá trị biểu thức tại \(x=-2\) là 2
Với \({x}<0\) khi rút gọn biểu thức ta được kết quả là \(2-{x}\)
Với \(0<{x}<2\) khi rút gọn biểu thức ta được kết quả là \({x}-2\)
Câu 14:
Cho \(\triangle \mathrm{ABC}\) tù tại A. Vẽ đường tròn \((\mathrm{O})\) đường kính AB, vẽ đường tròn \(\left(\mathrm{O}^{\prime}\right)\) đường kính AC. Đường thẳng AB cắt đường tròn \(\left(\mathrm{O}^{\prime}\right)\) tại điểm thứ hai D, đường thẳng AC cắt đường tròn \((\mathrm{O})\) tại điểm thứ hai E. Gọi F là giao điểm thứ hai của \((\mathrm{O})\) và \(\left(\mathrm{O}^{\prime}\right)\), H là giao điểm của AB và EF (F khác A).
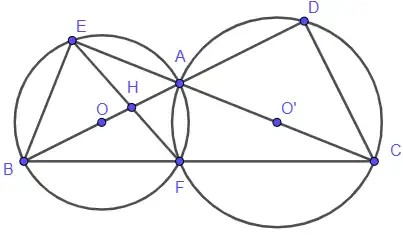
\(\mathrm{BH} . \mathrm{AD}=\mathrm{AH} . \mathrm{BD}\)
Ba điểm \(\mathrm{C}, \mathrm{B}, \mathrm{F}\) thẳng hàng
\(\frac{\mathrm{AD}}{\mathrm{AH}}=\frac{\mathrm{FH}}{\mathrm{FD}}\)
Bốn điểm \(\mathrm{B}, \mathrm{D}, \mathrm{C}, \mathrm{E}\) cùng nằm trên một đường tròn
Câu 15:
Cho biểu thức \(A=\sqrt{25{x}^2}-7 x\)
Với \(x<0\). Giá trị của \(x\) để giá trị biểu thức \(A=24\) là 2
Kết quả thực hiện phép tính biểu thức \(A\) là \(5|x|-7 {x}\)
Với \(x \geq 0\), kết quả rút gọn biểu thức \(A\) là \(2 x\)
Giá trị của biểu thức \(A\) tại \(x=-3\) là 36
Câu 16:
Cho phương trình \(\frac{x+2}{x}=\frac{2 x+3}{2(x-2)}\)
Phương trình đã cho vô nghiệm
Điều kiện xác định của phương trình là: \(x \neq 0\) và \(x \neq 2\)
Phương trình đã cho có một nghiệm duy nhất
\(x=\frac{-8}{3}\) là một nghiệm của phương trình đã cho
Câu 21:
Số nguyên lớn nhất thỏa mãn bất phương trình \(\frac{4 x-5}{-3}>\frac{7-x}{-5}\) là \(x=\ldots \)