Với giá trị nào của tham số m thì phương trình\((2+\sqrt{3})^{x}+(2-\sqrt{3})^{x}=m\) có hai nghiệm phân biệt?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa thấy \((2+\sqrt{3})(2-\sqrt{3})=1 \Leftrightarrow(2+\sqrt{3})^{x}(2-\sqrt{3})^{x}=1\)
Đặt \(t=(2+\sqrt{3})^{x} \Rightarrow(2-\sqrt{3})^{x}=\frac{1}{t}, \forall t \in(0,+\infty)\)
Khi đó \(PT\Leftrightarrow t+\frac{1}{t}=m \Leftrightarrow f(t)=t+\frac{1}{t}=m(2), \forall t \in(0,+\infty)\)
Xét hàm số \(f(t)=t+\frac{1}{t}\) xác định và liên tục trên \((0,+\infty)\)
Ta có \(f^{\prime}(t)=1-\frac{1}{t^{2}}=\frac{t^{2}-1}{t^{2}} . \text { Cho } f^{\prime}(t)=0 \Leftrightarrow t=\pm 1\)
Bảng biến thiên
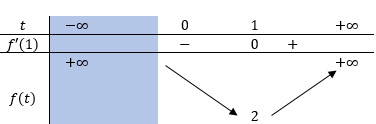
Dựa vào bảng biến thiên nếu m>2 thì (2) có hai nghiệm phân biệt \(\Rightarrow (2+\sqrt{3})^{x}+(2-\sqrt{3})^{x}=m\) có hai nghiệm phân biệt.














