ADMICRO
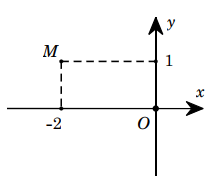
Gọi M , M' theo thứ tự là các điểm biểu diễn số phức . Trong các khẳng định sau, khẳng định nào là đúng?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo saiGọi M(a;b) là điểm biểu diễn số phức z .
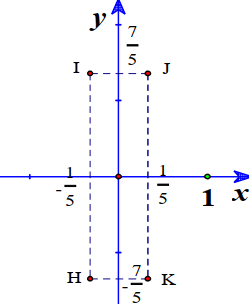
Ta có có điểm biểu diễn là
Suy ra
Ta có là tam giác vuông cân.
ZUNIA9
AANETWORK



.png)











