Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = {x^3} + mx – \frac{1}{{5{x^5}}}\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(y’ = 3{x^2} + m + \frac{1}{{{x^6}}}\)
Hàm số đồng biến trên \(\left( {0; + \infty } \right)\) khi và chỉ khi \(y’ = 3{x^2} + m + \frac{1}{{{x^6}}} \ge 0,\forall x \in \left( {0; + \infty } \right)\)
\( \Leftrightarrow – 3{x^2} – \frac{1}{{{x^6}}} \le m,\forall x \in \left( {0; + \infty } \right)\). Xét hàm số \(g(x) = – 3{x^2} – \frac{1}{{{x^6}}} \le m, x \in \left( {0; + \infty } \right)\)
\(g'(x) = – 6x + \frac{6}{{{x^7}}} = \frac{{ – 6({x^8} – 1)}}{{{x^7}}}, g'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = – 1{\rm{(loai)}}\end{array} \right.\)
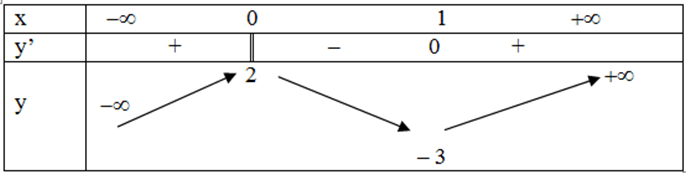
Bảng biến thiên:
.png)
Dựa vào BBT ta có \(m \ge – 4\), suy ra các giá trị nguyên âm của tham số m là – 4; – 3; – 2; – 1
Câu hỏi liên quan
-
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \([-100 ; 100]\) để hàm số \(y=(m-1) \sin x+(2 m+7) x\) đồng biến trên \(\mathbb{R}\)?
-
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 1\) nghịch biến trên các khoảng:
-
Cho hàm số \(y=(m+2) \frac{x^{3}}{3}-(m+2) x^{2}+(m-8) x+m^{2}-1\). Tìm tất cả các giá trị của tham số thực m để hàm số nghịch biến trên \(\mathbb{R} \text { ?}\)
-
Cho hàm số y=f(x) có đồ thị f '(x) như hình vẽ
Hàm số \(f\left(x^{2}\right)\) đồng biến khoảng nào dưới đây?
-
Hàm số \(y = {x^2} + 2x\) đồng biến trên các khoảng:
-
Tìm tất cả các giá trị của tham số m để hàm số \(y=x^{3}-6 x^{2}+m x+3\) đồng biến trên khoảng \((0 ;+\infty)\)?
-
Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) và có đồ thị hàm số y=f'(x) như hình vẽ.
Đặt \(g(x)=f\left(x^{2}-2\right)\) Mệnh đề nào dưới đây sai?
-
Với giá trị nào của m thì hàm số \(y=x^{3}-6 x^{2}+m x+1\) đồng biến trên khoảng \((0;+\infty)\)
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên R?
\(y' = - \frac{1}{3}{x^3} - m{x^2} + \left( {2m - 3} \right)x - m + 2\)
-
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây.
Hỏi có bao nhiêu giá trị nguyên của tham số m để phương trình \(f(3 \cos x+1)=-\frac{m}{2}\) có nghiệm trên đoạn -
Hàm số \(y=\frac{x+2}{x-1}\)nghịch biến trên các khoảng:
-
Tìm tất cả các giá trị thực của tham số để hàm số \(y = \frac{{{\rm{cos}}\,x – 3}}{{{\rm{cos }}x – m}}\) nghịch biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\)
-
Cho hàm số y=f(x) . Hàm số \(y=f^{\prime}\left(3 x-\frac{1}{2}\right)\) nghịch biến trên khoảng có đồ thị như hình bên. Hàm số \(y=f(2 x-1)\) nghịch biến trên khoảng:
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y\; = \;\frac{{x - m + 2}}{{x + 1}}\) giảm trên các khoảng mà nó xác định ?
-
Hàm số y=f(x) có đồ thị hàm số y=f'(x) như hình vẽ. Hỏi đồ thị hàm số \(y=f(2x^2+1)\) đồng biến trong khoảng nào dưới đây?
-
Hàm số \(y = {x^2} + 2x\) nghịch biến trên các khoảng:
-
Cho hàm số \(y\; = \frac{{x + 1}}{{x - 1}}\;\left( 1 \right)\)
Khẳng định nào sau đây là khẳng định đúng?
-
Cho hàm số \(y=x^{3}+2(m+1) x^{2}-3 m x+5-m\) với m là tham số. tìm diều kiện của m đẻ hàm số đồng biến trên tập xác định?
-
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2-3x+2 ≤ 0 cũng là nghiệm của bất phương trình mx2+(m+1) x+m+1 ≥ 0.
-
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{\cot x-1}{m \cot x-1}\) đồng biến trên khoảng \(\left(\frac{\pi}{4} ; \frac{\pi}{2}\right)\)
