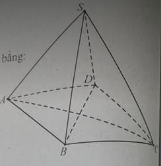
Cho hình chóp tứ giác đều S.ABCD có AB = SA = 2a. Khoảng cách từ đường thẳng AB đến (SCD) bằng bao nhiêu?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi I, M lần lượt là trung điểm cạnh AB và CD thì \(CD \bot (SIM)\)
Vẽ \(IH \bot SM\) tại \(H \in SM\) thì \(IH \bot (SCD)\)
\( \Rightarrow d\left( {AB,(SCD)} \right) = d\left( {I,(SCD)} \right) = IH = \frac{{SO.IM}}{{SM}}\)
\(\Delta SAB\) đều cạnh \(2a \Rightarrow SI = a\sqrt 3 \Rightarrow SM = a\sqrt 3 \)
Và \(OM = \frac{1}{2}IM = a \Rightarrow SO = \sqrt {S{M^2} - O{M^2}} = a\sqrt 2 \)
Cuối cùng \(d\left( {AB,(SCD)} \right) = \frac{{SO.IM}}{{SM}} = \frac{{a\sqrt 2 .2a}}{{a\sqrt 3 }} = \frac{{2a\sqrt 6 }}{3}\)
Câu hỏi liên quan
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông \(BD=2a,\Delta SAC\) vuông tại S và nằm trong mặt phẳng vuông góc với đáy, \(SC=a\sqrt{3}\). Khoảng cách từ điểm B đến mặt phẳng (SAD) là:
-
Cho hình chóp tứ giác đều có độ dài cạnh bên và cạnh đáy cùng bằng a. Khi đó, khoảng cách h giữa đường thẳng AD và mặt phẳng (SBC) là:
-
Cho hình chóp S.ABC có \(\Delta ABC\) đều cạnh a. Cạnh bên \(SA = a\sqrt 3 \) và vuông góc với \(\left( {ABC} \right)\). Khoảng cách từ điểm A đến mặt phẳng \(\left( {SBC} \right)\) bằng
-
Khối chóp S.ABC có đáy tam giác vuông cân tại B và \(AB=a.\,SA\bot \left( ABC \right)\). Góc giữa cạnh bên SB và mặt phẳng (ABC) bằng 600. Khi đó khoảng cách từ A đến (SBC) là:
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Gọi M là điểm thuộc SC sao cho MC=2MS. Biết AB=3, BC=\(3\sqrt{3}\). Khoảng cách giữa hai đường thẳng AC và BM là:
-
Cho lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông, \(AB=BC=1,AA'=\sqrt{2}\). M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AM; B'C.
-
Cho lăng trụ \(ABC.ABC\) các mặt đều là hình vuông cạnh a. Gọi D là trung điểm của cạnh \(BC.\) Tính khoảng cách giữa hai đường thẳng A’B’ và DC’ theo a
-
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt đá; \(BC=9m,AB=10m,AC=17m\). Biết thể tích khối chóp S.ABC bằng 73m3. Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B biết \(BC=a\sqrt{3}\), \(BA=a\). Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AC và biết thể tích khối chóp S.ABC bằng\(\frac{{{a}^{3}}\sqrt{6}}{6}\). Khoảng cách h từ C đến mặt phẳng (SAB) là.
-
Cho hình chóp SABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC vuông tại C và có BC = a, Tính khoảng cách từ B đến mặt phẳng \(\left( {SAC} \right)\).
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB' và AC bằng
-
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm \(I;AB = a;BC = a\sqrt 3 \), tam giác SAC vuông tại S. Hình chiếu vuông góc của S xuống mặt phẳng đáy trùng với trung điểm H của đoạn AI. Khoảng cách từ điểm C đến mặt phẳng (SAB) tính theo a bằng
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ A đến mặt phẳng \(\left( {SBD} \right)\) bằng
.png)
-
Cho hình lăng trụ ABC.A'B'C' có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30o. Hình chiếu H của A trên mặt phẳng (A'B'C') thuộc đường thẳng B'C'. Khoảng cách giữa hai mặt phẳng đáy là:
-
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi cạnh a, \(\widehat{BAD}={{120}^{0}}\) và \(AC'=a\sqrt{5}\). Khoảng cách giữa hai đường thẳng AB’ và BD là:
-
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AC = a, I là trung điểm SC. Hình chiếu vuông góc của S lên \(\left( {ABC} \right)\) là trung điểm H của BC. Mặt phẳng \(\left( {SAB} \right)\) tạo với \(\left( {ABC} \right)\) một góc \(60^\circ \). Tính khoảng cách từ I đến mặt phẳng \(\left( {SAB} \right)\).
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SBvuông góc với mặt phẳng đáy. Cho biết SB = 3a , AB = 4a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, biết \(SA \bot \left( {ABC} \right)\) và AB = 2a, AC = 3a, SA = 4a. Khoảng cách từ điểm A đến mặt phẳng \(\left( {SBC} \right)\) bằng
-
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có \( AB = a\sqrt 2 \). Cạnh bên SA = 2a và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ D đến mặt phẳng (SBC)
-
Xét tứ diện (OABC ) có (OA ), (OB ), (OC ) đôi một vuông góc. Gọi \(\alpha, \beta, \gamma \) lần lượt là góc giữa các đường thẳng (OA ), (OB ), (OC ) với mặt phẳng (ABC) (hình vẽ).
Khi đó giá trị nhỏ nhất của biểu thức \( M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\)
