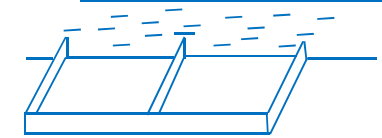
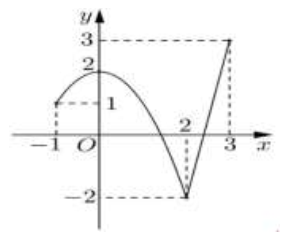
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên dưới.
.jpg.png)
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số \(g\left( x \right) = f\left( {2\sin \frac{x}{2}\cos \frac{x}{2} + 3} \right)\) trên \(\mathbb{R}.\) Giá trị của M + m bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t = 2\sin \frac{x}{2}\cos \frac{x}{2} + 3 = \sin x + 3.\)
Ta có: \(\forall x \in \mathbb{R} \Rightarrow t \in \left[ {2;4} \right].\)
Từ đồ thị ta thấy: \(\forall t \in \left[ {2;4} \right] \Rightarrow 1 \le f\left( t \right) \le 5 \Rightarrow \left\{ \begin{array}{l}M = \mathop {\max }\limits_\mathbb{R} g\left( x \right) = 5\\m = \mathop {\min }\limits_\mathbb{R} g\left( x \right) = 1\end{array} \right. \Rightarrow M + m = 6.\)



.jpg.png)
.jpg.png)
.png)











