Cho hàm số f(x) có bảng xét dấu đạo hàm f'(x) như sau:
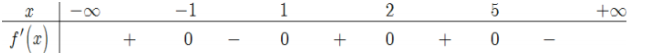
Hàm số \(y=3 f(-x+2)+e^{x^{3}+3 x^{2}-9 x+1}\) nghịch biến trên khoảng nào dưới đây?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(y^{\prime}=\left(3 f(-x+2)+\mathrm{e}^{x^{3}+3 x^{2}-9 x+1}\right)^{\prime}=-3 f^{\prime}(-x+2)+\left(3 x^{2}+6 x-9\right) e^{x^{3}+3 x^{2}-9 x+1}\)
Đặt \(t=-x+2 \Rightarrow x=2-t\)
khi đó \(y^{\prime}=-3 f^{\prime}(t)+3\left(t^{2}-6 t+5\right) \cdot e^{-t^{3}+9 t^{2}-15 t+3}\)
Ta có bảng xét dấu
Suy ra với \(t \in[1 ; 5] \text { thì } y^{\prime} \leq 0\)
\(t \in[1 ; 5] \Rightarrow 1 \leq-x+2 \leq 5 \Leftrightarrow-3 \leq x \leq 1\)
Vậy hàm số \(y=3 f(-x+2)+\mathrm{e}^{x^{3}+3 x^{2}-9 x+1}\) nghịch biến trên (-3;1).
Suy ra hàm số nghịch biến trên (-2;1) .
Câu hỏi liên quan
-
Cho hàm số y = f(x) = x4+ 2mx2+ m. Tìm m để f(x) > 0 với mọi m.
-
Cho hàm số \(f(x)=\frac{(m-1) x-1}{m x+2 m+1}\). Có bao nhiêu giá trị nguyên m để hàm số nghịch biến trên khoảng \((0 ;+\infty) ?\)
-
Hàm số \(y = \sqrt {2018x – {x^2}} \) nghịch biến trên khoảng nào trong các khoảng sau đây?
-
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}( x)=x^{2} (1-4 x^{2}), \quad \forall x \in \mathbb{R}\) . Hàm số y=f(cos x) đồng biến trên khoảng nào dưới đây?
-
Cho hàm số y = f(x) xác định trên R và có đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = mf(x) = m có đúng hai nghiệm phân biệt.
-
Tìm tất cả giá trị thực của tham số m để hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcLbAacaWG5b % Gaeyypa0JcdaWcaaqaaKqzGgGaaGymaaGcbaqcLbAacaaIZaaaaiaa % dIhakmaaCaaaleqabaGaaG4maaaajugObiabgkHiTiaaikdacaWGTb % GaamiEaOWaaWbaaSqabeaacaaIYaaaaKqzGgGaey4kaSIaaiikaiaa % d2gacqGHRaWkcaaIZaGaaiykaiaadIhacqGHRaWkcaWGTbGaeyOeI0 % IaaGynaaaa!4EA4! y = \frac{1}{3}{x^3} - 2m{x^2} + (m + 3)x + m - 5\) đồng biến trên R
-
Cho hàm số \(y=\frac{m x+2 m+3}{x+m}\) với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên
của m để hàm số nghịch biến trên khoảng \((2 ;+\infty)\) . Tìm S . -
Tìm tất cả các giá trị thực của m để hàm số\(y=\left(m^{2}+2 m+1\right) x+\left(m^{2}-m+1\right) \cos x\) luôn đồng biến trên \((0 ; 2 \pi)\).
-
Tính các giá trị của tham số m để hàm số \(y=\frac{\sin x-3}{\sin x-m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{4}\right)\).
-
Cho hàm số \(f(x)=\frac{(m-1) x-m}{x+2 m}\). Có bao nhiêu giá trị nguyên m thuộc khoảng \([-2019 ; 2020]\) để hàm số đồng biến trên khoảng \((-\infty ; 0) ?\)
-
Tập hợp tất cả các giá trị thực của tham số $m$ để hàm số \(y = \frac{{x + 4}}{{x + m}}\) đồng biến trên khoảng \(\left( { – \infty \,;\, – 7} \right)\) là
-
Gọi là tập hợp các số nguyên để hàm số \(y=f(x)=\frac{x+2 m-3}{x-3 m+2}\) đồng biến trên khoảng \((-\infty ;-14)\) . Tính tổng T của các phần tử trong S ?
-
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y=f'(x)\) như hình bên dưới.
Hỏi hàm số \(g(x)=f(1-x)+\frac{x^{2}}{2}-x\) nghịch biến trên khoảng nào? -
Hàm số nào sau đây đồng biến trên R.
-
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau
Đặt \(g(x)=f\left(\frac{x-1}{2}\right)-\frac{1}{3} x^{3}+\frac{3}{2} x^{2}-2 x+3\) . Mệnh đề nào dưới đây sai?
-
Cho hàm số \(y = {x^3} – 3{x^2}\). Mệnh đề nào dưới đây đúng?
-
Hàm số nào sau đây có bảng biến thiên như hình dưới?
-
Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.
-
Hàm số \(y = - {x^3} - 2{x^2} + 3x\) đồng biến trên các khoảng:
-
Hàm số \(y=\frac{x^{2}-4 x}{x+m}\) đồng biến trên \([1 ;+\infty)\) thì giá trị của m là:
