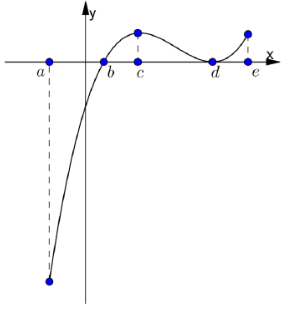
Cho hàm số có f(x) có đạo hàm là hàm \(f^{\prime}(x)\). Đồ thị hàm số \(f^{\prime}(x)\) như hình vẽ bên. Biết rằng \(f(0)+f(1)-2 f(2)=f(4)-f(3)\) . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]?

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{2{x^2} + x – 2}}{{2 – x}}\) trên đoạn \(\left[ { – 2;\,1} \right]\) lần lượt bằng:

Hàm số \(y=\frac{1}{x}+\frac{1}{x+1}+\frac{1}{x+2}\) đạt giá trị lớn nhất trên đoạn [-5 ;-3] bằng:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên dưới.

Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số \(g\left( x \right) = f\left( {2\sin \frac{x}{2}\cos \frac{x}{2} + 3} \right)\) trên \(\mathbb{R}.\) Giá trị của M + m bằng

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y =  - 3 + \sqrt {4 - {x^2}} \) lần lượt là

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\frac{x-1}{2x+1}\)trên đoạn [1;3] là:

Cho \(f\left( x \right) = \frac{1}{{{x^2} – 4x + 5}} – \frac{{{x^2}}}{4} + x\). Gọi \(M = \mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right)\), khi đó M–m bằng.

Gọi M là giá trị lớn nhất của hàm số \(\begin{equation} f(x)=4 \sqrt{x^{2}-4 x+6}+4 x-x^{2}+1 \end{equation}\) . Tính tích các nghiệm của phương trình f(x)=M?

Giá trị nhỏ nhất của hàm số \(y=x^{3}-3 x+5\) trên đoạn [0;2] là:

Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy. Hỏi chiều cao h (dm) của bồn là để ít tốn vật liệu nhất. Gần với giá trị nào nhất

Giá trị lớn nhất của hàm số \(y=\sqrt{x+4}+\sqrt{4-x}-4 \sqrt{(x+4)(4-x)}+5\)  bằng

Cho hàm số \(f\left( x \right) = \frac{{x – {m^2}}}{{x + 8}}\) với m là tham số thực. Giả sử \({m_0}\) là giá trị dương của tham số m để hàm số có giá trị nhỏ nhất trên đoạn \(\left[ {0;3} \right]\) bằng – 3. Giá trị \({m_0}\) thuộc khoảng nào trong các khoảng cho dưới đây?

Biết rằng giá trị lớn nhất của hàm số \(y = \left| {{x^2} + 2x + m – 4} \right|\) trên đoạn \(\left[ { – 2;\,1} \right]\) đạt giá trị nhỏ nhất, giá trị của tham số m bằng

Cho hàm số y = f(x) có đạo hàm cấp hai trên \(\mathbb{R}\). Biết f'(0) = 3,f'(2) = – 2018 và bảng xét dấu của f”(x) như sau:

Hàm số y = f(x + 2017) + 2018x đạt giá trị nhỏ nhất tại điểm \({x_0}\) thuộc khoảng nào sau đây?

Giá trị nhỏ nhất của hàm số \(f(x)=\frac{x^{2}-x+1}{x-1}\) trên khoảng \((1 ;+\infty)\) là

Cho hàm số \(f(x) = \left| {{x^4} – 8{x^2} – m} \right|.\) Có bao nhiêu giá trị nguyên của \(m \in {\rm{[}} – 50;50]\) sao cho với mọi số thực \(a, b, c \in {\rm{[}}0;3]\) thì \(f(a),{\rm{ }}f(b),{\rm{ }}f(c)\) là độ dài ba cạnh của một tam giác.

Giá trị nhỏ nhất của hàm số \(y=\sqrt{2} \cos 2 x+4 \sin x\) trên đoạn \(\left[0 ; \frac{\pi}{2}\right]\) là:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = – {x^2} – 1\). Với các số thực dương a, b thỏa mãn a < b, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\) bằng.

\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{x - 11}}{{x + 2}}\text{ trên đoạn } \left[ { - 1;3} \right]\)

Khu chung cư Royal City có 250 căn hộ cho thuê. Nếu người ta cho thuê x căn hộ thì lợi nhuận hàng tháng, tính theo triệu đồng, được cho bởi: \(P\left( x \right)\; = \; - 8{x^2}\; + \;3200x\;--\;80000.\). Hỏi lợi nhuận tối đa họ có thể đạt được là bao nhiêu?

Để giá trị lớn nhất của hàm số \(y = \left| {\sqrt {2x – {x^2}} – 3m + 4} \right|\) đạt giá trị nhỏ nhất thì m thỏa