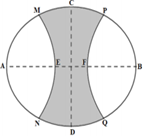
Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có 4 đỉnh \(A,\,B,\,C,\,D\) và 2 đường parabol có các đỉnh lần lượt là \(E,\,F\) (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng \(AB\), đối xứng nhau qua trục \(CD\), hai parabol cắt elip tại các điểm \(M,\,N,\,P,\,Q\). Biết \(AB=8\,m,\,CD=6\,m, \) \(MN=PQ=3\sqrt{3}\,m,\,EF=2\,m\). Chi phí để trồng hoa trên vườn là \(300.000\)đ/\({{m}^{2}}\). Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn hệ trục tọa độ \(Oxy\), như hình vẽ.
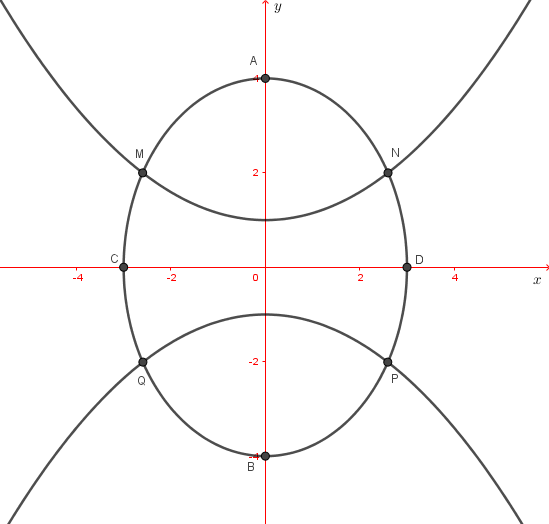
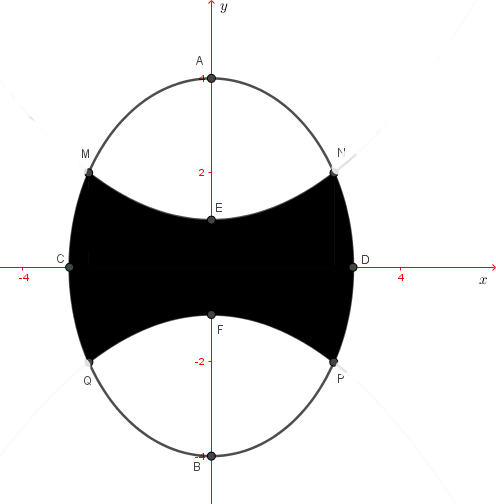
Ta có: \(CD=2a=6\Rightarrow a=3;\,AB=2b=8\Rightarrow b=4\Rightarrow \left( E \right):\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1.\)
Giả sử phương trình parabol phía trên trục \(Ox\) là \(\left( P \right):y=\text{a}{{x}^{2}}+bx+c, \) do điểm \(F\left( 0;1 \right)\) là đỉnh của \(\left( P \right)\Rightarrow b=0;c=1\),\(\Rightarrow y=\text{a}{{x}^{2}}+1\).
Mà \(\left( P \right)\cap \left( E \right)=\left\{ M,N \right\},\,\,MN=3\sqrt{3}\Rightarrow N(\frac{3\sqrt{3}}{2};2).\)
\(N\in \left( P \right)\Rightarrow 2=a{{\left( \frac{3\sqrt{3}}{2} \right)}^{2}}+1\Leftrightarrow a=\frac{4}{27}\Rightarrow y=\frac{4}{27}{{x}^{2}}+1\).
Do có tính đối xứng của \(\left( E \right),\,\left( P \right)\), suy ra diện tích cần tìm là
\(S=4\left( \left| \int\limits_{0}^{\frac{3\sqrt{3}}{2}}{\left( \frac{4}{27}{{x}^{2}}+1 \right)\text{d}x} \right|+\left| \int\limits_{\frac{3\sqrt{3}}{2}}^{3}{\left( 4\sqrt{1-\frac{{{x}^{2}}}{9}} \right)\text{d}x} \right| \right)\approx 16.03\,{{m}^{2}}\).
\(\Rightarrow \) Số tiền trồng hoa cho cả vườn hoa là: \(16.03\text{x}300.000=4.809.000\) đồng.
Chọn D.
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Ngô Quyền
Câu hỏi liên quan
-
Cho hàm đa thức bậc ba \(y=f\left( x \right)\) liên tục, có đạo hàm trên \(\left[ -2;2 \right]\) và có đồ thị như hình:
Số điểm cực tiểu của hàm số \(y=\sqrt[3]{{{\left( f\left( x \right) \right)}^{2}}}\) là?
-
Hãy tính Môđun của số phức \(z=\left( -4+3i \right).i\)?
-
Cho HS \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right]\). Gọi \(D\) là hình phẳng giới hạn bởi ĐTHS \(y=f\left( x \right)\), trục hoành và 2 đường thẳng \(x=a,\ x=b\). Thể tích khối tròn xoay được tạo thành khi quay \(D\) quanh trục hoành được tính theo công thức?
-
Cho HS \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(2f\left( \sin x-\cos x \right)=m-1\) có hai nghiệm phân biệt trên khoảng \(\left( -\frac{\pi }{4}\,;\,\frac{3\pi }{4} \right)\)?
-
Trong không gian với hệ tọa độ \(Oxyz\), cho mp \(\left( P \right):x+3y-2z+2=0\) và đường thẳng \(d:\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-4}{1}\). Đường thẳng qua \(A\left( 1;2;-1 \right)\) và cắt \(\left( P \right)\) và \(d\) lần lượt là tại \(B,\,\,C\left( a;b;c \right)\) sao cho \(C\) là trung điểm \(AB\). Giá trị biểu thức \(a+b+c\) bằng?
-
Tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| 5z \right|=\left| \left( 4+3i \right)z-25 \right|\) là đường thẳng có pt?
-
Cho một hộp chứa 7 quả cầu xanh, 5 quả cầu vàng (các quả cầu đôi một khác nhau). Chọn ngẫu nhiên 3 quả cầu từ hộp, tính xác suất để 3 quả được chọn có ít nhất 2 quả xanh?
-
Tìm họ các nguyên hàm của hàm số sau \(y={{e}^{x}}+2x\)?
-
Trong không gian với hệ tọa độ \(\text{O}xyz\), cho các điểm \(A\left( 1;0;0 \right)\), \(B\left( 0;2;0 \right)\),\(C\left( 0;0;4 \right)\). Viết PTĐT \(\Delta \) đi qua trực tâm \(H\) của tam giác \(\Delta ABC\) và vuông góc với mặt phẳng \(\left( ABC \right)\)?
-
Cho hình chóp \(S.ABC\text{D}\) có đáy \(ABC\text{D}\) là hình vuông cạnh \(a\). Tam giác \(SAB\) vuông tại \(S\) và nằm trong mp vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\text{D}\) bằng?
-
Cho khối tứ diện \(ABCD\) có thể tích \(V\). Gọi \(V'\) là thể tích của khối tám mặt có các đỉnh là trung điểm các cạnh của khối đa diện \(ABCD\). Tính tỉ số giữa \(\frac{V'}{V}\) bằng?
-
Tính tổng \(T\) tất cả các nghiệm thực của phương trình sau \({{4.9}^{x}}-{{13.6}^{x}}+{{9.4}^{x}}=0\)?
-
Trong không gian \(Oxyz\), điểm nào dưới đây thuộc đường thẳng \(d:\frac{x}{2}=\frac{y+1}{-3}=\frac{z}{1}\)?
-
Trong không gian \(Oxyz\), mặt phẳng \((\alpha ):5x-7y-z+2=0\) nhận vectơ nào dưới đây làm vectơ pháp tuyến?
-
Cho cấp số nhân sau \(({{u}_{n}})\) có \({{u}_{1}}=2,\text{ }{{u}_{4}}=-54\). Tìm công bội \(q\)?
-
Cho hàm bậc ba \(f\left( x \right)\) có đồ thị hàm số như hình vẽ:
Biết hàm số \(f\left( x \right)\) đạt cực trị tại hai điểm \({{x}_{1}},{{x}_{2}}\) thỏa mãn \({{x}_{2}}={{x}_{1}}+2\) và \(f\left( {{x}_{1}} \right)+f\left( {{x}_{2}} \right)=2\). Gọi \({{S}_{1}},{{S}_{2}}\) là diện tích của hai hình phẳng được cho trong hình vẽ bên. Tính tỉ số \(\frac{{{S}_{1}}}{{{S}_{2}}}\)?
-
Cho \(\int\limits_{-2}^{2}{f\left( x \right)dx}=9\) và \(\int\limits_{1}^{2}{f\left( x \right)dx}=2\) thì giá trị của \(\int\limits_{-2}^{1}{f\left( x \right)\text{d}x}\) bằng?
-
Một vật chuyển động theo quy luật \(s=-\frac{1}{3}{{t}^{3}}+6{{t}^{2}}\) với \(t\) (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \(s\) (mét) là quãng đường vật di chuyển trong khoảng thời gian đó. Hỏi trong khoảng thời gian \(7\) giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bao nhiêu?
-
Hàm số \(y=f\left( x \right)\) có đồ thị như hình. Giá trị của \(\int\limits_{-2}^{2}{f\left( x \right)dx}\) bằng?
-
Phương trình \({{z}^{2}}+az+b=0;(a,b\in \mathbb{R})\) có nghiệm phức là \(3+4i\). Tính giá trị của \(a+b\)?
