Tìm tất cả các giá trị thực của tham số \(m\) để pt \(x{{\log }_{3}}\left( x+1 \right)={{\log }_{9}}\left[ 9{{\left( x+1 \right)}^{2m}} \right]\) có 2 nghiệm phân biệt?

A. \(m\in \left( -1\,;\,0 \right)\).

B. \(m\in \left( -2\,;\,0 \right)\).

C. \(m\in \left( -1\,;\,+\infty \right)\).

D. \(m\in \left[ -1\,;\,0 \right)\).

Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Chủ đề: Đề thi THPT QG

Môn: Toán

Lời giải:

Báo sai

- Cách 1:

Điều kiện: \(x>-1\).

Ta có pt: \(x{{\log }_{3}}\left( x+1 \right)={{\log }_{9}}\left[ 9{{\left( x+1 \right)}^{2m}} \right]\Leftrightarrow x{{\log }_{3}}\left( x+1 \right)=1+m{{\log }_{3}}\left( x+1 \right)\)

\(\Leftrightarrow \left( x-m \right){{\log }_{3}}\left( x+1 \right)=1\) (1).

Đặt: \({{\log }_{3}}\left( x+1 \right)=t\Rightarrow x={{3}^{t}}-1\)

Ta có, Pt (1) \(\Rightarrow \left( {{3}^{t}}-m-1 \right).t=1\Rightarrow f\left( t \right)={{3}^{t}}-\frac{1}{t}-1=m\), với \(t\ne 0\).

Đặt: \(f\left( t \right)={{3}^{t}}-\frac{1}{t}-1\), với \(t\ne 0\).

\(\Rightarrow f'\left( t \right)={{3}^{t}}.\ln 3+\frac{1}{{{t}^{2}}}>0\,,\,t\in \left( -\infty \,;\,0 \right),\,\left( 0\,;\,+\infty \right)\).

Suy ra, \(f\left( t \right)={{3}^{t}}-\frac{1}{t}-1\) là hàm số đồng biến trên \(\left( -\infty \,;\,0 \right)\) và \(\left( 0\,;\,+\infty \right)\).

Ta xét các giới sau:

\(\underset{t\to -\infty }{\mathop{\lim }}\,\left( {{3}^{t}}-\frac{1}{t}-1 \right)=-1\), \(\underset{t\to +\infty }{\mathop{\lim }}\,\left( {{3}^{t}}-\frac{1}{t}-1 \right)=+\infty \).

\(\underset{t\to {{0}^{+}}}{\mathop{\lim }}\,\left( {{3}^{t}}-\frac{1}{t}-1 \right)=-\,\infty \), \(\underset{t\to {{0}^{-}}}{\mathop{\lim }}\,\left( {{3}^{t}}-\frac{1}{t}-1 \right)=+\,\infty \).

Ta có bảng biến thiên của hàm số \(f\left( t \right)={{3}^{t}}-\frac{1}{t}-1\), với \(t\in \left( -\infty \,;\,0 \right),\,\left( 0\,;\,+\infty \right)\).

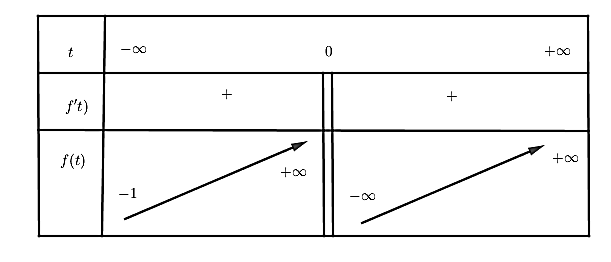
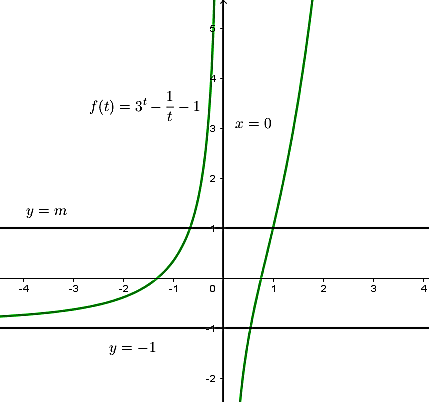
Ta có, số nghiệm của Pt (1) cũng chính là số nghiệm của đồ thị hàm số (C) \(f\left( t \right)={{3}^{t}}-\frac{1}{t}-1\)

và đồ thị hàm số\(y=m\) (song song hoặc trùng với trục hoành).

Dựa, vào đồ thị ở hình vẽ trên, để phương trình \(x{{\log }_{3}}\left( x+1 \right)={{\log }_{9}}\left[ 9{{\left( x+1 \right)}^{2m}} \right]\) có ba nghiệm khi \(m\in \left( -\,1;\,+\infty \right)\).

- Cách 2:

Điều kiện: \(x>-1\).

Ta có: \(x{{\log }_{3}}\left( x+1 \right)={{\log }_{9}}\left[ 9{{\left( x+1 \right)}^{2m}} \right]\)(1)

Nhận thấy \(x=0\) không là nghiệm phương trình trên.

Pt (1) \(\Leftrightarrow \left( x-m \right){{\log }_{3}}\left( x+1 \right)=1\Leftrightarrow x-\frac{1}{{{\log }_{3}}\left( x+1 \right)}=m\).

Đặt: \(f\left( x \right)=x-\frac{1}{{{\log }_{3}}\left( x+1 \right)}\Rightarrow f'\left( x \right)=1+\frac{1}{\left( x+1 \right)\ln 3.{{\left( {{\log }_{3}}\left( x+1 \right) \right)}^{2}}}>0,\,\forall x\in \left( -1\,;\,+\infty \right)\).

Suy ra \(f\left( x \right)=x-\frac{1}{{{\log }_{3}}\left( x+1 \right)}\) là hàm số đồng biến \(\forall x\in \left( -1\,;\,+\infty \right)\).

Ta có BBT của hàm số \(f\left( x \right)=x-\frac{1}{{{\log }_{3}}\left( x+1 \right)}\).

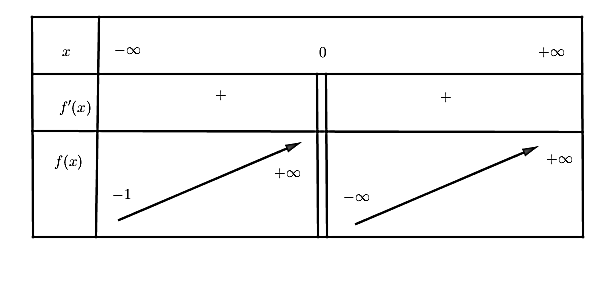
Dựa, vào BBT ở hình vẽ trên, để phương trình \(x{{\log }_{3}}\left( x+1 \right)={{\log }_{9}}\left[ 9{{\left( x+1 \right)}^{2m}} \right]\) có ba nghiệm khi \(m\in \left( -\,1;\,+\infty \right)\).

Chọn C.

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài