Cho hình lăng trụ ABC.A′B′C′ có AA′=AB′=AC′. Tam giác ABC vuông cân tại A có BC=2a. Khoảng cách từ A′ đến mặt phẳng (BCC′B′) là a√33. Tính thể tích khối lăng trụ đã cho?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai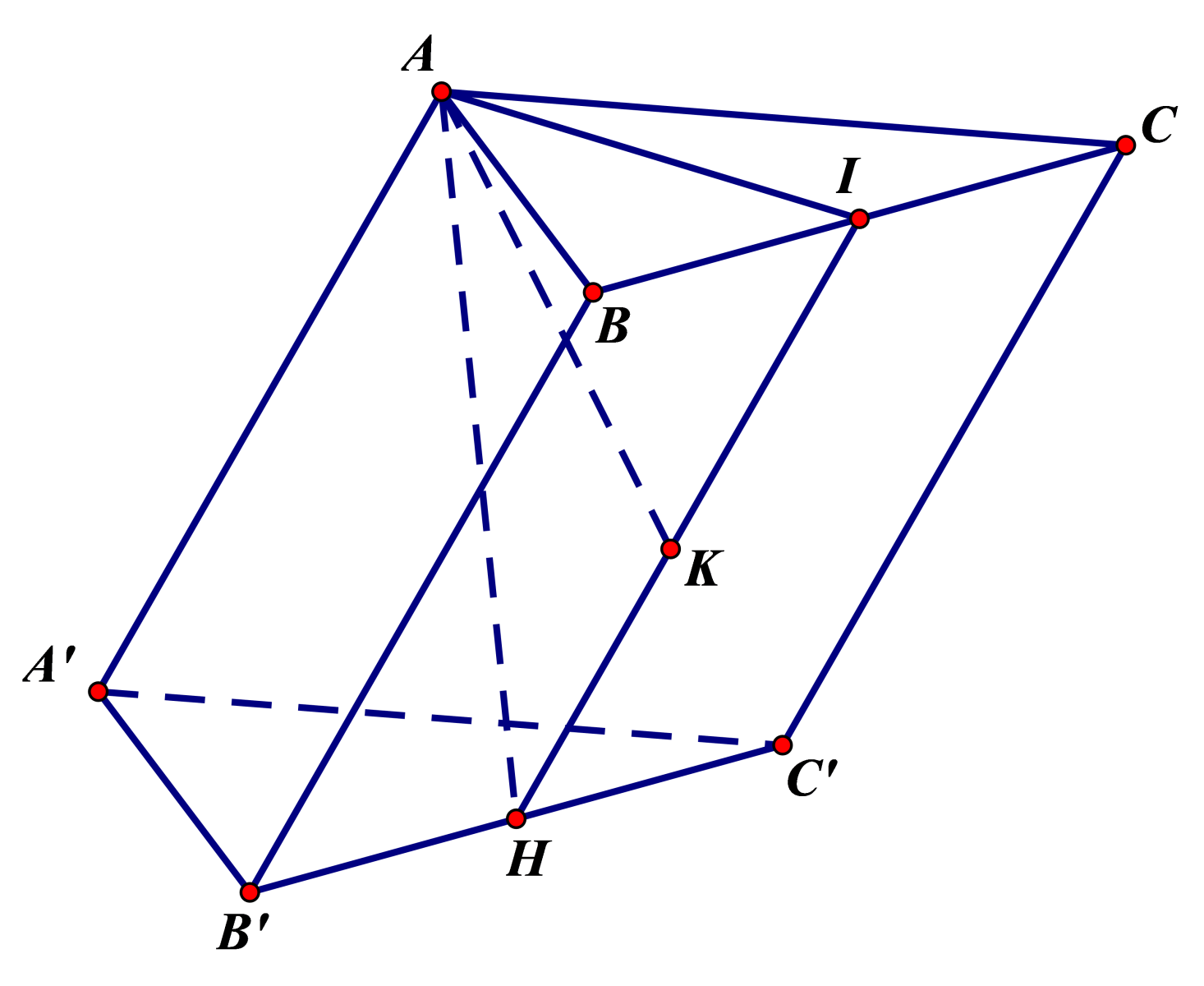
Gọi Hlà trung điểm B′C′. Vì tam giác A′B′C′là tam giác vuông cân tại A′ nên Hlà tâm đường tròn ngoại tiếp tam giác A′B′C′.
Mặt khác AA′=AB′=AC′, từ đó suy ra A,Hcách đều 3 điểm A′,B′,C′ hay AH⊥(A′B′C′).
Gọi Ilà trung điểm của BC khi đó AI⊥BC(1)
Mà B′C′⊥AH và BC//B′C′ suy ra BC⊥AH(2)
Từ (1) và (2) ta suy ra BC⊥(AHI)⇒(BCC′B′)⊥(AHI) theo giao tuyến là HI (3)
Kẻ AK⊥HI, ta được AK⊥(BCC′B′) hay d(A′,(BCC′B′))=d(A,(BCC′B′))=AK=a√33
Xét tam giác AIH vuông tại A, ta được 1AH2=1AK2−1AI2=3a2−1a2=2a2⇒AH=a√22
Vậy thể tích khối lăng trụ V=a√22⋅12.(a√2)2=a3√22.
Chọn A
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Ngô Quyền