Cho hình chóp \(S.ABC\text{D}\) có đáy \(ABC\text{D}\) là hình vuông cạnh \(a\). Tam giác \(SAB\) vuông tại \(S\) và nằm trong mp vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\text{D}\) bằng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai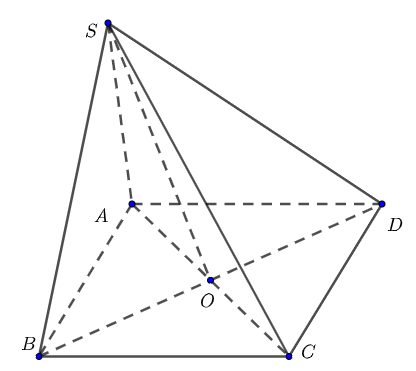
Ta có \(\left\{ \begin{align}
& \left( SAB \right)\bot \left( ABC\text{D} \right) \\
& \left( SAB \right)\cap \left( ABC\text{D} \right)=AB \\
& BC\bot AB \\
\end{align} \right.\,\,\Rightarrow BC\bot \left( SAB \right)\Rightarrow BC\bot SA\) \(\left( 1 \right)\)
Mà tam giác \(SAB\) vuông tại \(S\)\(\Rightarrow SB\bot SA\) \(\left( 2 \right)\).
Từ \(\left( 1 \right);\left( 2 \right)\Rightarrow SA\bot \left( SBC \right)\Rightarrow SA\bot SC\).
Gọi \(O\) là tâm hình vuông \(ABC\text{D}\), khi đó ta được \(OA=OB=OC=OS=\frac{a\sqrt{2}}{2}\).
\(O\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\text{D}\);
Thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\text{D}\)bằng \(V=\frac{4}{3}\pi {{\left( \frac{a\sqrt{2}}{2} \right)}^{3}}=\frac{\pi {{a}^{3}}\sqrt{2}}{3}\).
Chọn B
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Ngô Quyền