Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với đáy, \(SC=a\sqrt{3}\). Gọi \(M,\,N,P,\,Q\) lần lượt là trung điểm của \(SB,\,SD,CD,\,BC\). Tính thể tích của khối chóp\(A.MNPQ\)?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai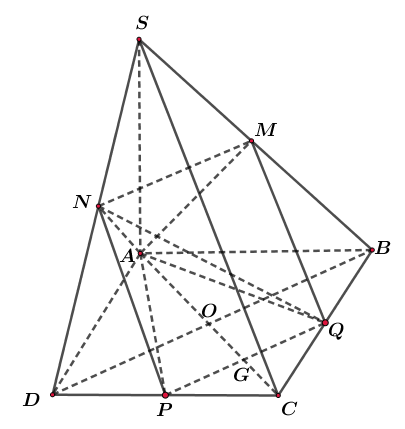
Gọi \(O=AC\cap BD;\,G=AC\cap PQ\)
Ta có \(\left. \begin{align}
& MQ\text{//}SC \\
& NP\text{//}SC \\
& MQ=NP=\frac{1}{2}SC \\
\end{align} \right\}\Rightarrow MQ=NP;MQ\text{//}NP\)
\(\Rightarrow MNPQ\) là hình bình hành \(\Rightarrow {{S}_{MNPQ}}=2{{S}_{\Delta NPQ}}\)
Ta có \(S{{A}^{2}}=S{{C}^{2}}-A{{C}^{2}}=3{{a}^{2}}-2{{a}^{2}}={{a}^{2}}\Rightarrow SA=a\)
Mà \(PQ=\frac{1}{2}BD=\frac{a\sqrt{2}}{2};\,\,AG=\frac{3}{4}AC=\frac{3}{4}.a\sqrt{2}=\frac{3a\sqrt{2}}{4}\)
\(\Rightarrow {{S}_{\Delta APQ}}=\frac{1}{2}AG.PQ=\frac{1}{2}.\frac{a\sqrt{2}}{2}.\frac{3a\sqrt{2}}{4}=\frac{3{{a}^{2}}}{8}\)
Khi đó \({{V}_{A.MNPQ}}=2.{{V}_{ANPQ}}=2.{{V}_{N.APQ}}=2.\frac{1}{2}{{V}_{S.APQ}}=\frac{1}{3}SA.{{S}_{\Delta APQ}}=\frac{1}{3}.a.\frac{3{{a}^{2}}}{8}=\frac{{{a}^{3}}}{8}\).
Chọn C
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Ngô Quyền