Trong không gian với hệ trục tọa độ \(Oxyz\), từ điểm \(A\left( 1;1;0 \right)\) kẻ các tiếp tuyến đến mặt cầu \(\left( S \right)\) có tâm \(I\left( -1;1;1 \right)\) và bán kính \(R=1\). Gọi \(M\left( a;b;c \right)\) là một trong các tiếp điểm ứng với các tiếp tuyến trên. Tìm GTLN của biểu thức \(T=\left| 2a-b+2c \right|\)?

A. \(\frac{3-2\sqrt{41}}{15}\).

B. \(\frac{3+2\sqrt{41}}{5}\).

C. \(\frac{3+\sqrt{41}}{5}\).

D. \(\frac{3+\sqrt{41}}{15}\).

Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Chủ đề: Đề thi THPT QG

Môn: Toán

Lời giải:

Báo sai

Phương trình mặt cầu \(\left( S \right)\):\({{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=1\).

Ta có \(\overrightarrow{IA}=\left( 2;0;-1 \right)\) nên \(AI=\sqrt{5}\) và \(AM=\sqrt{A{{I}^{2}}-{{R}^{2}}}=2\).

Vậy \(M\) thuộc mặt cầu \(\left( {{S}'} \right):{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{z}^{2}}=4\).

\(\Rightarrow\) \(M\) thuộc đường tròn \(\left( C \right)\) là giao tuyến giữa \(\left( S \right)\) và \(\left( {{S}'} \right)\).

\(\Rightarrow\)\(\left( C \right)\) thuộc mặt phẳng \(\left( P \right):2x-y+2=0\).

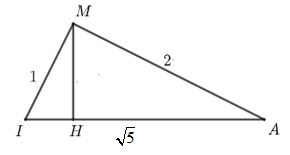
Gọi \(H\) là hình chiếu của \(M\) trên \(AI\) thì \(IH.IA=I{{M}^{2}}\Leftrightarrow \frac{IH}{IA}=\frac{I{{M}^{2}}}{I{{A}^{2}}}=\frac{1}{5}\).

Suy ra \(\overrightarrow{IH}=\frac{1}{5}\overrightarrow{IA}\) nên \(H\left( -\frac{3}{5};1;\frac{4}{5} \right)\) là tâm đường tròn \(\left( C \right)\).

Bán kính đường tròn \(\left( C \right)\) bằng \(r=MH=\sqrt{M{{I}^{2}}-I{{H}^{2}}}=\frac{2}{\sqrt{5}}\).

Gọi \(\left( Q \right)\) là mặt phẳng \(2x-y+2z=0\) và \(F\) là hình chiếu của \(H\) lên \(\left( Q \right)\).

Khi đó ta có \(HF=d\left( H,\left( Q \right) \right)=\frac{1}{5}\) và \(\cos \alpha =\frac{2}{3\sqrt{5}}\); với \(\alpha\) là góc giữa \(\left( P \right)\) và \(\left( Q \right)\). \(\Rightarrow \sin \alpha =\frac{\sqrt{41}}{3\sqrt{5}}\).

Gọi \(\left( d \right)\) là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\).

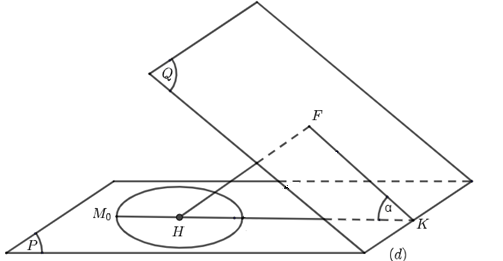
Gọi \(K\) là hình chiếu của \(H\) trên \(\left( d \right)\) nên \(HK=\frac{HF}{\sin \alpha }=\frac{3\sqrt{5}}{5\sqrt{41}}\).

Gọi \({{M}_{0}}\) là giao điểm tia đối \(HK\) cắt \(\left( C \right)\)\(\Rightarrow {{M}_{0}}K=HK+r=\frac{3\sqrt{5}}{5\sqrt{41}}+\frac{2}{\sqrt{5}}\).

Dễ dàng thấy với mọi \(M\in \left( C \right)\), khoảng cách lớn nhất từ \(M\) đến \(\left( Q \right)\) là \(d\left( {{M}_{0}};\left( Q \right) \right)\).

\(d\left( M;\left( Q \right) \right)={{M}_{0}}K.\sin \alpha =\left( \frac{3\sqrt{5}}{5\sqrt{41}}+\frac{2}{\sqrt{5}} \right)\frac{\sqrt{41}}{3\sqrt{5}}=\frac{3+2\sqrt{41}}{15}\)

Mặt khác \(d\left( M;\left( Q \right) \right)=\frac{\left| 2a-b+2c \right|}{3}\) nên \(T=3d\left( M;\left( Q \right) \right)\le 3d\left( {{M}_{0}};\left( Q \right) \right)=\frac{3+2\sqrt{41}}{5}\).

Chọn B

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài