Cho hàm số f x ( ) có bảng biến thiên như sau:
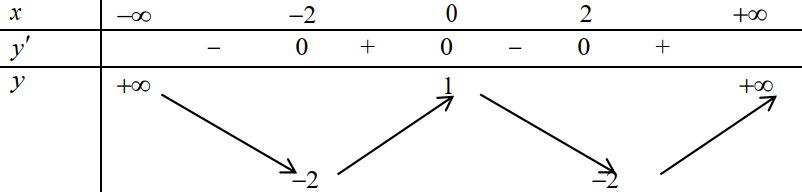
Gọi \(g(x)=\| 2 f(x)-2|+f(x)+10-m|\) có tổng giá trị nhỏ nhất và giá trị lớn nhất trên đoạn [-2 ; 2] bằng 2. Tính tích các phần tử của S .
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét hàm số \(g(x)=|| 2 f(x)-2|+f(x)+10-m| \text { trên đoạn }[-2 ; 2]\)
ta có: \(g(x)=\| 2 f(x)-2|+f(x)+10-m|=|-2 f(x)+2+f(x)+10-m|\) vì \(f(x) \leq 1 \quad \forall x \in[-2 ; 2]\)
Hay \(g(x)=|-f(x)+12-m|=|f(x)+m-12| \text { trên đoạn }[-2 ; 2]\)
Xét hàm số \(h(x)=f(x)+m-12\text{ trên đoạn }[-2 ; 2]\) ta có bảng biến thiên.
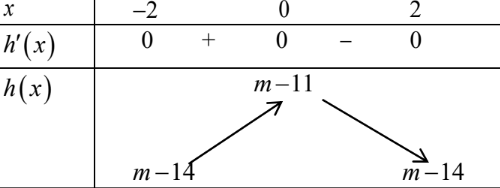
Ta thấy \(\underset{[-2 ; 2]}{\operatorname{Max}} g(x)=\operatorname{Max}\{|m-14| ;|m-11|\}\)
Theo đề bài ta có:
\(\operatorname{Max}_{[-2 ; 2]} g(x) \leq 2 \Leftrightarrow\left\{\begin{array}{l} |m-14| \leq 2 \\ |m-11| \leq 2 \end{array} \Leftrightarrow\left\{\begin{array}{l} -2 \leq m-14 \leq 2 \\ -2 \leq m-11 \leq 2 \end{array} \Leftrightarrow\left\{\begin{array}{l} 12 \leq m \leq 16 \\ 9 \leq m \leq 13 \end{array} \Leftrightarrow 12 \leq m \leq 13\right.\right.\right.\)
Từ đó ta có \(\left\{\begin{array}{l} m-11>0 \\ m-14<0 \end{array} . \text { Nên } \operatorname {Ming}(x)=0 \text { và } \operatorname{Max}\limits_{[-2 ; 2]} g(x)=2\right.\)\
Suy ra \(\left[\begin{array}{l} |m-14|=2 \\ |m-11|=2 \end{array} \Leftrightarrow\left[\begin{array}{l} m=16 \\ m=12 \\ m=13 \\ m=9 \end{array}\right.\right.\)
Vì \(12 \leq m \leq 13 \text { nên }\left[\begin{array}{l} m=13 \\ m=12 \end{array} . \text { Ta có: } 12.13=156\right.\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Nguyễn Trãi