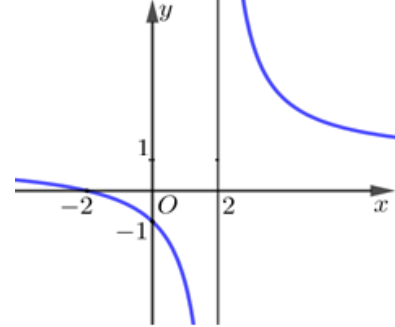
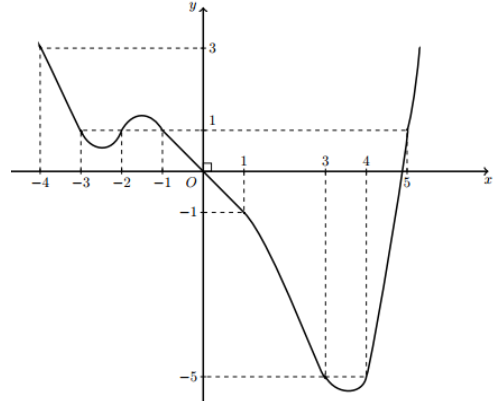
Cho hàm số y=f(x) có đồ thị như hình sau:
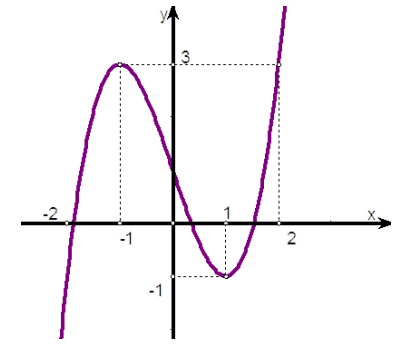
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình \( f(3 \sin x+m)-3=0\)có đúng 6 nghiệm phân biệt thuộc \([0 ; 3 \pi]\) Tổng các phần tử của S bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai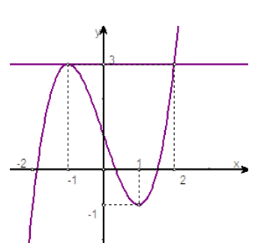
Ta có \(f(3 \sin x+m)-3=0 \Leftrightarrow f(3 \sin x+m)=3\)
Dụa vào đô thị ta có
\(f(3 \sin x+m)=3 \Leftrightarrow\left[\begin{array}{l} 3 \sin x+m=-1 \\ 3 \sin x+m=2 \end{array} \Leftrightarrow\left[\begin{array}{l} \sin x=\frac{-1-m}{3} \\ \sin x=\frac{2-m}{3}=1+\frac{-1-m}{3} \end{array}\right.\right.\)
Ta có đồ thị hàm số \(y=\sin x \text { trên }[0 ; 3 \pi]\) như sau
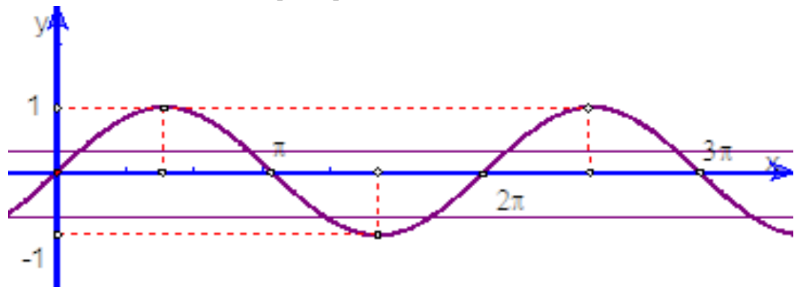
Dụa vào đồ thị để phương trình \(f(3 \sin x+m)-3=0\) có 6 nghiệm phân biệt thuộc \([0 ; 3 \pi]\) thì
\(\left\{\begin{array}{l} -1<\frac{-1-m}{3} \leq 0 \\ 0<\frac{2-m}{3} \leq 1 \end{array} \Leftrightarrow-1 \leq m<2\right.\)
Do \(m \in \mathbb{Z} \Rightarrow\left[\begin{array}{l} m=-1 \\ m=0 \Rightarrow S=0 \\ m=1 \end{array}\right.\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Nguyễn Trãi