Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a . Hình chiếu vuông góc của S trên mặt phẳng đáy ABCD là điểm H thuộc cạnh AB sao cho HB=2.HA . Cạnh SA hợp với mặt phẳng đáy góc \(60^0\) . Tính diện tích mặt cầu ngoại tiếp hình chóp S ABCD
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai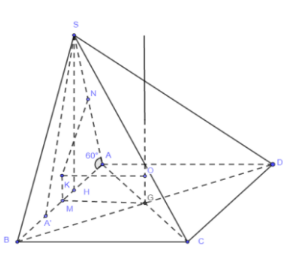
Goi G là tâm hình vuông A B C D ; M, N lần lươt là trung điểm AB, SA ; A' là điềm đối xứng cüa A qua H
Vì A' là điểm đối xứng của A qua H nên ta có HA=HA'
Suy ra SH là đường trung trực của AA'. Do đó \(\triangle S A A^{\prime}\) là tam giác cân.
Mà \(\widehat{S A A^{\prime}}=\widehat{(S A,(A B C D))}=60^{\circ} .\)
Do đó \(\Delta S A A^{\prime}\) là tam giác đều canh bằng 2a
Từ M kẻ đường trung trực của AB cắt A'N tại K . Khi đó K là tâm đường tròn ngoại tiếp \(\triangle S A B\)
Qua G dựng trục đương tròn ngoại tiếp Gy của hình vuông ABCD. Qua K dựng trục đường tròn ngoại tiếp Kx của \(\Delta S A B\). Goi\(O=K x \cap G y\) là tâm mặt cầu ngoại tiếp hình chóp \(S . A B C D\)
Ta có: \(A^{\prime} N=\sqrt{A A^{\prime 2}-A N^{2}}=a \sqrt{3} ; M A^{\prime}=\frac{a}{2}\)
Lại có \(\Delta M K A^{\prime} \sim \Delta N A A^{\prime} \Rightarrow \frac{A^{\prime} K}{A A^{\prime}}=\frac{M A^{\prime}}{N A^{\prime}}=\frac{\frac{a}{2}}{a \sqrt{3}}=\frac{\sqrt{3}}{6} \Rightarrow A^{\prime} K=\frac{\sqrt{3}}{6} A A^{\prime}=\frac{a \sqrt{3}}{3}\)
Mặt khác \(K O=M G=\frac{A D}{2}=\frac{3 a}{2}\)
Vậy diện tích mặt cầu ngoại tiếp là \(\frac{55 \pi a^{2}}{3}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Nguyễn Trãi
Câu hỏi liên quan
-
Thể tích khối cầu có bán kính r bằng
-
Gọi Alà tập các số tự nhiên có 5 chữ số đôi một khác nhau được lập từ các số 1;2;3;4;5;6;7;8;9. Lấy ngẫu nhiên một số thuộc tập A. Tính xác suất để số lấy được luôn có mặt hai chữ số 1;2 và chúng không đứng cạnh nhau
-
Cho hàm số y =f(x) có đồ thị như sau
Số nghiệm thực của phương trình \(f(|x|)-1=0\) là
-
Cho đường thẳng \(d: \frac{x-2}{-1}=\frac{y+1}{-1}=\frac{z+1}{1}\)-và mặt phẳng \((P): 2 x+y-2 z=0\). Đường thẳng \(\Delta\) nằm trong (P), cắt d và vuông góc với d có phương trình là:
-
Cho hình chóp \(S . A B C D\) có đáy là hình thoi cạnh a ,\(\widehat{ B A D}=60^{\circ},S B=S D=S C\) , M là trung điểm của SD , H là hình chiếu của S trên mặt phẳng (ABCD). Tính khoảng cách giữa hai đường thẳng SH và CM
-
Cho a là số thực dương khác 1 . Tính \(I=\log _{\sqrt{a}} a\)
-
Tính diện tích xung quanh của hình nón có bán kính đáy \(r=\sqrt{3}\) và chiều cao h = 4
-
Cho hình chóp S .ABCD có đáy là hình thang vuông tại A và B , \(S A \perp(A B C D), A D=3 a\), \(S A=A B=B C=a\) . Gọi S ' là điểm thỏa mãn \(\overrightarrow{S S^{\prime}}=\frac{1}{2} \overrightarrow{A B}\). Tính thể tích khối đa diện \(S S^{\prime} A B C D\)
-
Gọi F x ( ) là nguyên hàm của hàm số \(f(x)=\frac{x}{\sqrt{8-x^{2}}}\) thỏa mãn F(2)=0 . Khi đó phương trình F(x)=x có nghiệm là:
-
Tổng số đường tiệm cận ngang của đồ thị hàm số \(y=\frac{2 x-1}{x+1}\)
-
Hàm số \(y=x^{4}-2 x^{2}+1\)nghịch biến trên khoảng nào sau đây?
-
Gọi\(z_1, z_2\) , là các nghiệm phức của phương trình\(z^{2}+z+1=0, \text { đặt } \mathrm{w}=z_{1}^{2021}+z_{2}^{2021}\)1 Khi đó
-
COVID19 là một loại bệnh viêm đường hô hấp cấp do chủng mới virus corona (nCOV) bắt đầu từ Trung Quốc (đầu tháng 12/2019) gây ra với tốc độ truyền bệnh rất nhanh (tính đến ngày 02/06/2020 đã có 6.365.173 người nhiễm bệnh. Giả sử ban đầu có 1 người nhiễm bệnh và cứ sau 1 ngày sẽ lây sang a người khác (\(a \in \mathbb{N}^{*}\) ). Tất cả những người nhiễm bệnh lại lây sang những người khác với tốc độ như trên (1 người lây cho a người). Tìm a biết sau 7 ngày có 16384 người mắc bệnh. (Giả sử người nhiễm bệnh không phát hiện bản thân bị bệnh, không phòng tránh cách ly và trong thời gian ủ bệnh vẫn lây sang người khác được)
-
Cho số phức \(z=2-3 i\) . Phần ảo của số phức z là.
-
Trong không gian Oxyz , cho điểm \(A(1 ;-3 ; 2)\) Tọa độ điểm A' đối xứng với A điểm qua mặt phẳng (Oyz) là
-
Cho Hàm số f(x) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số y =f'(x)như hình vẽ bên dưới
Hàm số \(g(x)=f\left(\frac{5 x}{x^{2}+4}\right)\) có bao nhiêu điểm cực đại?
-
Cho hàm số \(y=x^{3}-3 x^{2}+9\) có đồ thị là (C). Điểm cực tiểu của đồ thị (C) là
-
Tất cả các giá trị của m để hàm số \(y=\frac{2 \cos x-1}{\cos x-m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right)\) là
-
Trong không gian Oxyz , mặt phẳng đi qua điểm M (1;2;3) và song song với mặt phẳng \((P): x-2 y+z-3=0\) có phương trình là
-
Cho lăng trụ đều ABC.A' B'C' có cạnh đáy bằng 2a, độ dài cạnh bên bằng \(a \sqrt{3}\) . Tính thể tích V của khối lăng trụ
