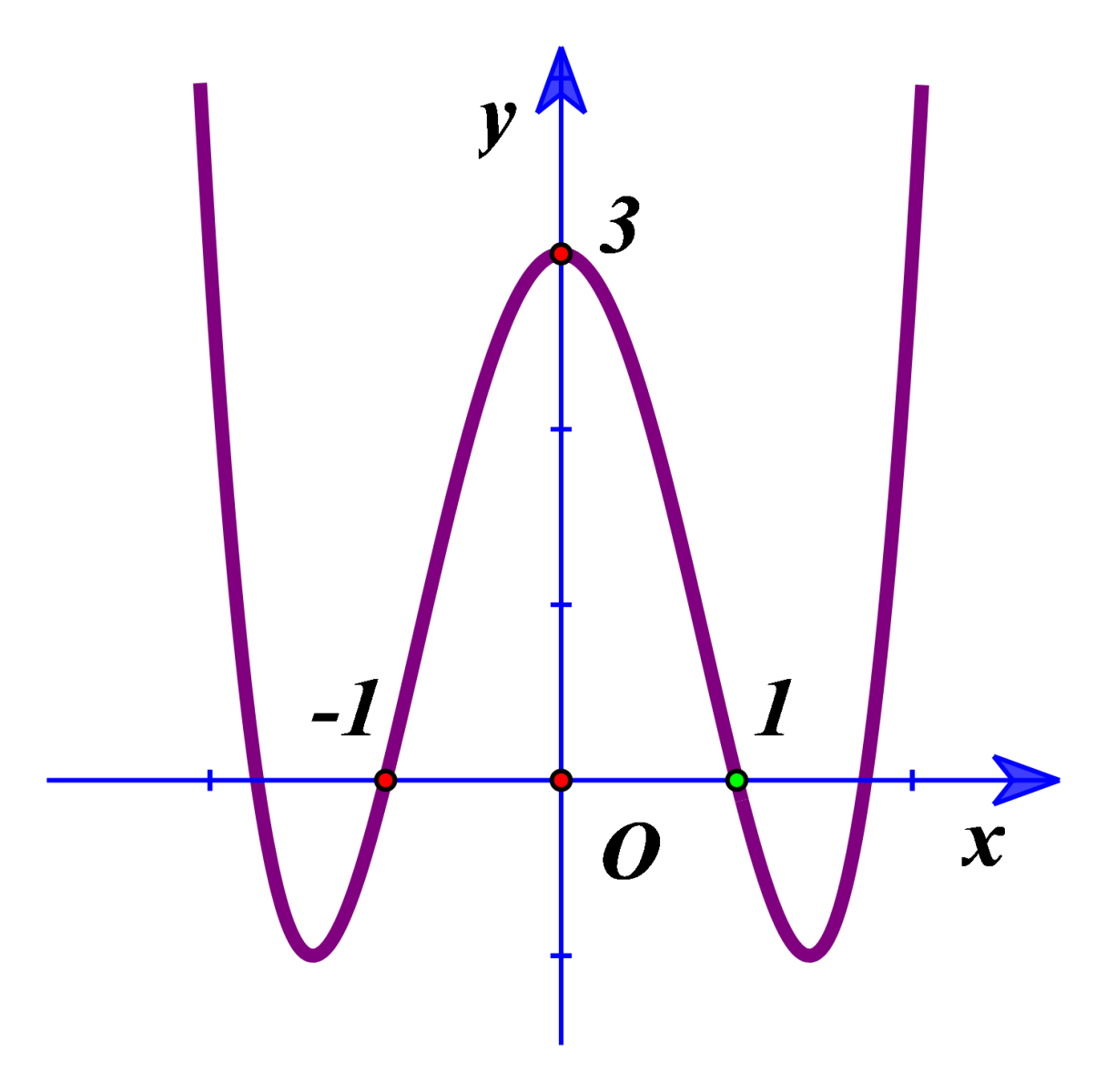
Cho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như hình dưới. Hàm số \(y={{e}^{3f\left( 2-x \right)+1}}+{{3}^{f\left( 2-x \right)}}\) đồng biến trên khoảng nào?

Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ 1\,;2 \right]\) thỏa mãn \(\int\limits_{1}^{2}{{{\left( x-1 \right)}^{2}}f\left( x \right)\text{d}x}=-\frac{1}{3}\), \(f\left( 2 \right)=0\) và \(\int\limits_{1}^{2}{{{\left[ {f}'\left( x \right) \right]}^{2}}\text{d}x}=7\). Tính tích phân của \(I=\int\limits_{1}^{2}{f\left( x \right)\text{d}x}\)?

Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số sau \(y={{x}^{3}}-3m{{x}^{2}}+3x-6{{m}^{3}}\) đồng biến trên khoảng \(\left( 0;\text{ }+\infty  \right)\) là?

Tìm tham số \(m\) để ĐTHS \(y=\frac{\left( m+1 \right)x-5m}{2x-m}\) có tiệm cận ngang là đường thẳng \(y=1\)?

Cho mặt cầu \(\left( S \right)\) có diện tích bằng \(4\pi \). Tính thể tích khối cầu \(\left( S \right)\)?

Cho biết \(\int\limits_{0}^{1}{f(x)\text{d}x}=-3\) và \(\int\limits_{0}^{1}{g(x)\text{d}x}=2\), khi đó \(\int\limits_{0}^{1}{\left[ f\left( x \right)+2g\left( x \right) \right]\text{d}x}\) bằng?

Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình sau:

Mệnh đề nào sau đây đúng về hàm số đó?

Môđun của số phức sau đây \(z=(-4+3i).i\) bằng?

Tính tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó bằng?

Trong không gian \(Oxyz\), cho điểm \(M\left( 2;1;1 \right)\), mp \(\left( \alpha  \right):x+y+z-4=0\) và mặt cầu \(\left( S \right):{{\left( x-3 \right)}^{2}}+{{\left( y-3 \right)}^{2}}+{{\left( z-4 \right)}^{2}}=16\). Phương trình đường thẳng \(\Delta \) đi qua \(M\) và nằm trong \(\left( \alpha  \right)\) cắt mặt cầu \(\left( S \right)\) theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng \(\Delta \) đi qua điểm nào trong các điểm sau đây?

Tổng tất cả các nghiệm của phương trình sau \({{\log }_{2}}\left| {{x}^{2}}+2x-3 \right|-{{\log }_{2}}\left| x+3 \right|=3\) bằng?

Trong không gian với hệ tọa độ \(Oxyz,\) cho 2 điểm \(A\left( 2;1;3 \right),B\left( 6;5;5 \right)\). Gọi \(\left( S \right)\) là mặt cầu đường kính \(AB\). Mặt phẳng \(\left( P \right)\) vuông góc với \(AB\) tại \(H\) sao cho khối nón đỉnh \(A\) và đáy là hình tròn tâm \(H\) là giao tuyến của \(\left( S \right)\) và \(\left( P \right)\) có thể tích lớn nhất, biết rằng \(\left( P \right):2x+by+cz+d=0\) với \(b,c,d\in \mathbb{Z}\). Tính \(S=b+c+d\)?

Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ:

Tập hợp tất cả giá trị thực của tham số \(m\) để phương trình \(f\left( 2\sin x+1 \right)=m\) có nghiệm thuộc nửa khoảng \(\left[ 0\,;\frac{\pi }{6} \right)\) là?

Cho \(\int\limits_{1}^{3}{\frac{\ln x}{{{\left( x+1 \right)}^{2}}}\text{dx}}=\frac{a}{b}\ln 3-c\ln 2\) với \(a,\text{ }b,\text{ }c\in \mathbb{N}*\) và phân số \(\frac{a}{b}\) tối giản. Tính giá trị của \(a+b+c\)?

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(\left( SAC \right)\bot \left( ABC \right)\) và \(AB=3a,\text{ }BC=5a\). Biết rằng \(SA=2a\sqrt{3}\) và \(\widehat{SAC}=30{}^\circ \). Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( SBC \right)\) bằng?

Tập nghiệm của BPT \({{\log }_{2}}\left( 4x+8 \right)-{{\log }_{2}}x\le 3\) là?

Cho hình chóp tứ giác \(S.ABCD\) có \(SA=SB=SC=SD=4\sqrt{11}\) và đáy \(ABCD\) là hình vuông cạnh \(8\). Thể tích của khối chóp \(S.ABC\) bằng?

Ký hiệu \({{z}_{1}},\text{ }{{z}_{2}}\) là 2 nghiệm phức của pt \({{z}^{2}}+2z+11=0\). Khi đó giá trị biểu thức \(A={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}\) bằng?

Cho phương trình \({{3}^{x}}\left( {{3}^{2x}}+1 \right)-\left( {{3}^{x}}+m+2 \right)\sqrt{{{3}^{x}}+m+3}=2\sqrt{{{3}^{x}}+m+3}\), với \(m\) là tham số. Có tất cả bao nhiêu giá trị nguyên âm của \(m\) để phương trình có nghiệm thực?

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), cạnh \(SA\) vuông góc với mp đáy và \(SA=2a\), gọi \(M\) là trung điểm của \(SC\). Tính côsin của góc \(\alpha \) là góc giữa đường thẳng \(BM\) và \(\left( ABC \right)\)?

Cho biết \(\int\limits_{-1}^{2}{f\left( x \right)}\text{d}x=2\) và \(\int\limits_{1}^{2}{f\left( x \right)}\text{d}x=5\), tích phân \(\int\limits_{1}^{2}{f\left( 3-2x \right)}\text{d}x\) bằng?