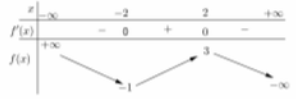
Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong hình bên.
.png)
Số nghiệm thực phân biệt của phương trình \(f\left( {{x^2}f(x)} \right) + 2 = 0\) là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{array}{l}
f\left( {{x^2}f(x)} \right) + 2 = 0 \Leftrightarrow f\left( {{x^2}f(x)} \right) = - 2 \Leftrightarrow \left[ \begin{array}{l}
{x^2}f(x) = 0{\rm{ (1)}}\\
{x^2}f(x) = {t_1} \in (0;1){\rm{ (2)}}\\
{x^2}f(x) = {t_2} \in (2;3){\rm{ (3)}}\\
{x^2}f(x) = {t_1} \in (3;4){\rm{ (4)}}
\end{array} \right.\\
+ (1) \Leftrightarrow \left[ \begin{array}{l}
{x^2} = 0\\
f(x) = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = {x_1} \in ( - 1;0)\\
x = {x_2} \in (3;4)
\end{array} \right.\\
+ (2) \Leftrightarrow f(x) = \frac{{{t_1}}}{{{x^2}}}
\end{array}\)
Hàm số \(g(x) = \frac{{{t_1}}}{{{x^2}}}\) có \(g'(x) = - \frac{{2{t_1}}}{{{x^3}}}.{\rm{ }}g'(x) > 0 \Leftrightarrow x < 0,{\rm{ }}g'(x) < 0 \Leftrightarrow x > 0.\)
Do đó đồ thị hàm số y = g(x) cắt đồ thị hàm số y = f(x) tại 2 điểm phân biệt nên (2) có 2 nghiệm phân biệt.
Tương tự, (3) cũng có 2 nghiệm phân biệt, (4) cũng có 2 nghiệm phân biệt. Dễ kiểm tra 6 nghiệm của (2), (3) và (4) là phân biệt và mỗi nghiệm bé hơn x1 hoặc lớn hơn x2.
Vậy số nghiệm thực phân biệt của phương trình \(f\left( {{x^2}f(x)} \right) + 2 = 0\) là 9.
Đề thi tốt nghiệp THPT môn Toán năm 2020
Bộ GD&ĐT mã đề 103
Câu hỏi liên quan
-
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên
.png)
Số nghiệm thực của phương trình f(x) = 1 là
-
Xét các số thực không âm x và y thỏa mãn \(2x + y{.4^{x + y - 1}} \ge 3\). Giá trị nhỏ nhất của biểu thức \(P = {x^2} + {y^2} + 2x + 4y\) bằng
-
Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập hợp \(\{ 1,2,3,4,5,6,7\} .\) Chọn ngẫu nhiên một số thuộc S, xác suất để số đó không có hai chữ số liên tiếp nào cùng chẵn bằng
-
Nghiệm của phương trình \({3^{x + 1}} = 9\) là
-
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(a\sqrt 2 \) và O là tâm của đáy. Gọi M, N, P, Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và S' là điểm đối xứng của S qua O. Thể tích của khối chóp S'.MNPQ bằng
-
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3\) và công bội q = 4 Giá trị của \({u_2}\) bằng
-
Cho a và b là hai số thực dương thỏa mãn \({9^{{{\log }_3}\left( {ab} \right)}} = 4a\). Giá trị của \(a{b^2}\) bằng
-
\(\int {{x^4}} dx\) bằng
-
Cho hàm số \(f(x) = \frac{x}{{\sqrt {{x^2} + 1} }} \cdot \)
Họ tất cả các nguyên hàm của hàm số \(g(x) = (x + 1)f'(x)\) là
-
Trong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {(z - 1)^2} = 16.\) Bán kính của (S) bằng
-
Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x - 3}}{4} = \frac{{y + 1}}{{ - 2}} = \frac{{z + 2}}{3}.\) Vectơ nào dưới đây là một vectơ chỉ phương của d?
-
Cho khối hộp chữ nhật có ba kích thước 2; 6; 7. Thể tích của khối hộp đã cho bằng
-
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = \frac{{x + 2}}{{x + m}}\) đồng biến trên khoảng \(( - \infty ; - 5)\) là
-
Cho hình trụ có bán kính đáy r = 5 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã cho bằng
-
Trong không gian Oxyz, cho ba điểm \(A(1;2;0),B(1;1;2)\) và \(C(2;3;1)\) . Đường thẳng đi qua A và song song với BC có phương trình là
-
Cho hàm số f(x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
-
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
.png)
-
Với a,b là các số thực dương tùy ý và \(a \ne 1,{\log _{{a^3}}}b\) bằng
-
Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn \){\log _3}\left( {{x^2} + y} \right) \ge {\log _2}(x + y)?\)
-
Trong không gian Oxyz, cho điểm \(M(2; - 1;2)\) và đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = \frac{{z - 3}}{1}.\) Mặt phẳng đi qua điểm M và vuông góc với d có phương trình là
