Cho đồ thị \(\left( C \right):y=\frac{x}{x-1}\). Đường thẳng \(d\) đi qua điểm \(I\left( 1;1 \right)\) cắt \(\left( C \right)\) tại 2 điểm phân biệt \(A\) và \(B\). Khi diện tích tam giác \(MAB\) đạt giá trị nhỏ nhất, với \(M\left( 0;3 \right)\) thì độ dài đoạn \(AB\) bằng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi \(A\left( 1-m;\frac{1-m}{-m} \right);B\left( 1+m;\frac{m+1}{m} \right)\) với \(m>0\).
\(I\left( 1;1 \right)\) là tâm đối xứng của đồ thị hàm số, suy ra \(I\) là trung điểm của \(A,B\).
\({{S}_{\Delta MAB}}=2{{S}_{\Delta MIB}}\) nên \({{S}_{\Delta MAB}}\min \) khi \({{S}_{\Delta MIB}}\) min.
Phương trình đường thẳng \(MI:2x+y-3=0\).
Ta có
\({{S}_{MIB}}=\frac{1}{2}ah=\frac{1}{2}d\left( B;IM \right).IM=\frac{1}{2}\left| \frac{2{{m}^{2}}-m+1}{m} \right|\)
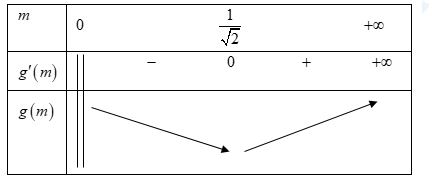
Xét hàm số \(g\left( m \right)=\frac{2{{m}^{2}}-m+1}{m}\)
\({g}'\left( m \right)=\frac{2{{m}^{2}}-1}{{{m}^{2}}}\)
Ta có bảng biến thiên
Suy ra \(\underset{m>0}{\mathop{\min \left| g\left( m \right) \right|}}\,=2\sqrt{2}-1\) khi \(m=\frac{1}{\sqrt{2}}\).
Khi đó \(IB=\sqrt{{{m}^{2}}+\frac{1}{{{m}^{2}}}}=\sqrt{\frac{5}{2}}\) suy ra \(AB=2IB=\sqrt{10}\).
Chọn A
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Thủ Thiêm



.png)
.PNG)
.PNG)
.PNG)











