Cho hàm số \(f\left( x \right)\) là hàm số đa thức bậc bốn. Biết \(f\left( 0 \right)=0\) và ĐTHS \(y={f}'\left( x \right)\) có hình vẽ:
.PNG)
Tập nghiệm của phương trình \(f\left( \left| 2\sin x-1 \right|-1 \right)=m\) (với \(m\) là tham số) trên đoạn \(\left[ 0;3\pi\right]\) có tất cả bao nhiêu phần tử?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐồ thị đã cho là đồ thị hàm số bậc ba có hai điểm cực trị \(x=0\) và \(x=2\) nên có dạng \({f}'\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\).
Lần lượt thay thế các dữ kiện từ hình vẽ, ta được
\(\begin{array}{l} \left\{ \begin{array}{l} d = 2\\ c = 0\\ 3 \cdot a \cdot {2^2} + 2 \cdot b \cdot 2 = 0\\ - {a^3} + b + d = - 2 \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l} a = 1\\ b = - 3\\ c = 0\\ d = 2 \end{array} \right. \end{array}\)
Suy ra \({f}'\left( x \right)={{x}^{3}}-3{{x}^{2}}+2\)\( \Rightarrow f\left( x \right)=\frac{{{x}^{4}}}{4}-{{x}^{3}}+2x+C\).
Mà \(f\left( 0 \right)=0\)\( \Rightarrow C=0\Rightarrow f\left( x \right)=\frac{{{x}^{4}}}{4}-{{x}^{3}}+2x\).
Ta có \({f}'\left( x \right)=0\)
\(\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=1-\sqrt{3} \\ & x=1+\sqrt{3} \\ \end{align} \right.\)
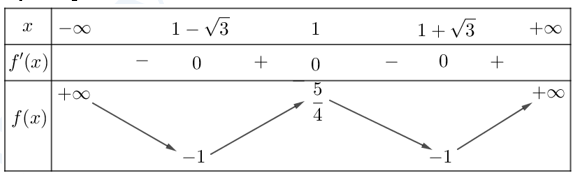
Suy ra bảng biến thiên
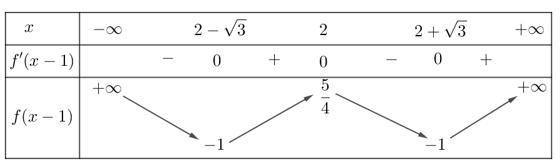
Từ đó ta có bảng biến thiên của \(f\left( x-1 \right)\)
Vì \(-1\le \sin x\le 1,\forall x\in \left[ 0;3\pi\right]\) nên \(0\le \left| 2\sin x-1 \right|\le 3\).
Đặt \(t=\left| 2\sin x-1 \right|\), \(t\in \left[ 0;3 \right]\)
Dựa vào bảng biến thiên, suy ra phương trình \(f\left( t-1 \right)=m\) có tối đa \(2\) nghiệm \(t=h\), \(t=k\).
Do đó
\(\begin{array}{l} \left[ \begin{array}{l} 2\sin x - 1 = \pm h\\ 2\sin x - 1 = \pm k \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} \sin x = \frac{{ \pm h + 1}}{2}\\ \sin x = \frac{{ \pm k + 1}}{2} \end{array} \right. \end{array}\)
Trên \(\left[ 0;3\pi\right]\), mỗi phương trình có nhiều nhất \(4\) nghiệm, do đó phương trình đã cho có nhiều nhất \(16\) nghiệm.
Chọn D
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Thủ Thiêm
Câu hỏi liên quan
-
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), \(O\) là tâm mặt đáy. Khoảng cách giữa 2 đường thẳng \(SO\) và \(CD\) bằng?
-
Cho khối chóp \({S.ABCD}\) có đáy \({ABCD}\) là hình thoi, \({\widehat{DAB}=60{}^\circ }\), \({AD=a}\), tam giác \({SBC}\) cân tại \({S}\), tam giác \({SCD}\) vuông tại \({C}\), k/c giữa \({SA}\) và \({CD}\) bằng \({\frac{4a}{5}}\). Thể tích của khối chóp đã cho bằng?
-
Cho các số thực dương sau \(a\,,\,b\) thỏa mãn \({{\log }_{2}}\left( a+b \right)=3+{{\log }_{2}}ab\). Giá trị \(\frac{1}{a}+\frac{1}{b}\) bằng?
-
Xét tất cả các số thực dương \(x;y\) thỏa \(\frac{x+y}{10}+\log \left( \frac{1}{2x}+\frac{1}{2y} \right)=1+2xy\). Khi biểu thức \(\frac{4}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}\) đạt giá trị nhỏ nhất, tích \(xy\) bằng?
-
Họ các nguyên hàm của HS \(f(x)=\sin 3x\) là?
-
Giả sử \(f\left( x \right)\) là hàm có đạo hàm liên tục trên khoảng \(\left( 0;\pi \right)\) và \(f'\left( x \right)\sin x=x+f\left( x \right)\cos x,\,\,\,\forall x\in \left( 0;\pi \right).\) Biết \(f\left( \frac{\pi }{2} \right)=1,\,\,f\left( \frac{\pi }{6} \right)=\frac{1}{12}\left( a+b\ln 2+c\pi \sqrt{3} \right)\), với \(a,\,\,b,\,\,c\) là các số nguyên. Giá trị \(a+b+c\) bằng?
-
Hàm số \(f\left( x \right)={{x}^{4}}{{\left( x-1 \right)}^{2}}\) có tất cả bao nhiêu điểm cực trị?
-
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình. Hỏi phương trình \(2f\left( x \right)=5\) có bao nhiêu nghiệm trên đoạn \(\left[ -1;2 \right]\)?
-
Cho các số phức sau \(z=2+i\) và \(w=3-i.\) Phần thực của số phức \(z+w\) bằng?
-
Giả sử hàm số \(f\left( x \right)\) có đạo hàm liên tục trên. Biết rằng \(G\left( x \right)={{x}^{3}}\) là 1 nguyên hàm của \(g\left( x \right)={{e}^{-2x}}f\left( x \right)\) trên \(\mathbb{R}\). Họ tất cả các nguyên hàm của \({{e}^{-2x}}{f}'\left( x \right)\) là?
-
Cho \(10\) học sinh gồm \(5\) bạn lớp \(12A\) và \(5\) bạn lớp \(12B\) tham gia một trò chơi. Để thực hiện trò chơi, người điều khiển ghép ngẫu nhiên \(10\) học sinh đó thành \(5\) cặp. Xác suất để không có cặp nào gồm hai học sinh cùng lớp bằng?
-
Cho hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) (với \(a,b,c,d\in \mathbb{R}\)) có đồ thị như hình:
.PNG)
Có bao nhiêu số dương trong các số \(a,b,c,d\)?
-
Cho góc ở đỉnh của 1 hình nón bằng \({{60}^{0}}\). Gọi \(r,h,l\) lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
-
Cho CSC \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=1\) và \({{u}_{3}}=\frac{1}{3}\). Công sai của \(\left( {{u}_{n}} \right)\) bằng?
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình. Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ -3;3 \right]\) bằng?
.png)
-
Trong không gian \(Oxyz\), đường thẳng \(\Delta \) đi qua \(A\left( -1;-1;1 \right)\) và nhận \(\overrightarrow{u}=\left( 1;2;3 \right)\) làm VTCP có phương trình chính tắc là?
-
Có tất cả bao nhiêu số phức \(z\) đôi một khác nhau thỏa mãn \(\left| z+i \right|=2\) và \({{\left( z-2 \right)}^{4}}\) là số thực?
-
Cho HS \(f\left( x \right)\) nhận giá trị dương và có đạo hàm liên tục trên \(\left[ 1;\ e \right]\). Biết \(f\left( 1 \right)=1\) và \(x.f\left( x \right).{f}'\left( x \right)={{x}^{2}}+{{f}^{2}}\left( x \right)\) với mọi \(x\in \left[ 1;\ e \right].\) Khi đó, \(\int\limits_{1}^{e}{\frac{f\left( x \right)}{{{x}^{2}}}dx}\) bằng?
-
Cho khối lăng trụ tam giác \(ABC.{A}'{B}'{C}'\) có cạnh \(A{A}'=2a\) và tạo với mp đáy 1 góc bằng \(60{}^\circ \), diện tích tam giác \(ABC\) bằng \({{a}^{2}}\). Thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\) bằng?
-
Tìm tập xác định của hàm số \(y=\log x+\log \left( 3-x \right)\)?
