Có tất cả bao nhiêu giá trị nguyên dương của mm không vượt quá 2021 để phương trình 4x−1−m.2x−2+1=04x−1−m.2x−2+1=0 có nghiệm?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương pháp:
- Đặt ẩn phụ t=2x−2>0t=2x−2>0.
- Cô lập mm, đưa phương trình về dạng m=g(t)(t>0)m=g(t)(t>0).
- Lập BBT của hàm số g(t)g(t) khi t>0t>0.
- Dựa vào BBT tìm giá trị của mm để phương trình có nghiệm.
Cách giải:
Ta có 4x−1−m.2x−2+1=0⇔4.(2x−2)2−m.2x−2+1=04x−1−m.2x−2+1=0⇔4.(2x−2)2−m.2x−2+1=0.
Đặt t=2x−2>0t=2x−2>0, phương trình đã cho trở thành 4t2−mt+1=0⇔m=4t2+1t=g(t)(t>0)4t2−mt+1=0⇔m=4t2+1t=g(t)(t>0).
Xét hàm số g(t)=4t2+1t=4t+1tg(t)=4t2+1t=4t+1t có g′(t)=4−1t2=0⇔t=12g′(t)=4−1t2=0⇔t=12.
BBT:
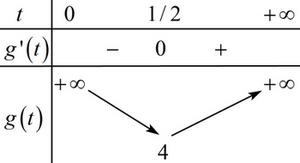
Dựa vào BBT ta thấy phương trình có nghiệm t>0⇔m≥4t>0⇔m≥4.
Kết hợp điều kiện {m∈Z+m≤2021⇒m∈{4;5;6;...;2020;2021}.
Vậy có 2018 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn B.
Đề thi giữa HK2 môn Toán 12 năm 2023-2024
Trường THPT Lạc Long Quân