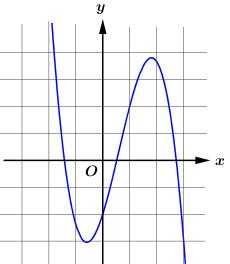
Cho hàm số sau \(y = {x^3} - 3m{x^2} + 4{m^3}.\) Với giá trị nào của \(m\) để hàm số có 2 điểm cực trị A,B sao cho \(AB = \sqrt {20}\)?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương pháp:
- Giải phương trình \(y' = 0\) tìm 2 điểm cực trị của đồ thị hàm số theo \(m\).
- Sử dụng công thức \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \), giải phương trình tìm \(m\).
Cách giải:
+ Điều kiện tồn tại cực trị:
\(y' = 3{x^2} - 6mx = 0\) có 2 nghiệm phân biệt \({x_1};{x_2}\)
\( \Leftrightarrow 3x\left( {x - 2m} \right) = 0\) có 2 nghiệm phân biệt \({x_1};{x_2}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x_1} = 0}\\{{x_2} = 2m \ne 0 \Leftrightarrow m \ne 0}\end{array}} \right.\)
+ Khi đó \(\left\{ {\begin{array}{*{20}{l}}{A\left( {0;4{m^3}} \right)}\\{B\left( {2m;0} \right)}\end{array}} \right. \Rightarrow A{B^2} = {\left( {{x_B} - {x_A}} \right)^2} + {\left( {{y_B} - {y_A}} \right)^2} \Leftrightarrow 4{m^2} + 16{m^6} = 20\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 4{m^6} + {m^2} - 5 = 0}\\{ \Leftrightarrow {m^2} = 1}\\{ \Leftrightarrow m = {\rm{\;}} \pm 1}\end{array}\)
Chọn C.
Đề thi giữa HK2 môn Toán 12 năm 2023-2024
Trường THPT Lạc Long Quân
Câu hỏi liên quan
-
Nghiệm của phương trình sau \({3^{x - 1}} = 9\) là?
-
Tập nghiệm của bất phương trình sau \({\log _{\dfrac{1}{3}}}\dfrac{{1 - 2x}}{x} > 0\) có dạng \(\left( {a;b} \right)\). Tính \(T = 3a - 2b\)?
-
Cho 3 điểm \(A\left( {2;1; - 1} \right),\)\(B\left( { - 1;0;4} \right),\)\(C\left( {0; - 2; - 1} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với BC có phương trình là?
-
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(\int\limits_0^7 {f\left( x \right)dx} {\rm{\;}} = 10\) và \(\int\limits_0^3 {f\left( x \right)dx} {\rm{\;}} = 6\). Tính giá trị của \(I = \int\limits_{ - 2}^3 {f\left| {3 - 2x} \right|dx} \)?
-
Ngày 20/01/2020, bà T gửi 100 triệu đồng vào ngân hàng theo hình thức lãi kép và lãi suất 0,7%/ tháng. Ngày 20/5/2020, lãi suất ngân hàng thay đổi với lãi suất mới là 0,75% mỗi tháng. Hỏi đến ngày 20/8/2020, số tiền bà T nhận về (cả vốn và lãi) gần nhất với số nào sau đây?
-
Tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi đường thẳng \(3x - 2\) và ĐTHS \(y = {x^2}\) quanh trục Ox?
-
Tìm nguyên hàm của hàm số sau \(f(x) = 3{x^2} + 8\sin x\)?
-
Viết PTTT của đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x - 2}}\), biết tiếp tuyến có hệ số góc \(k = {\rm{\;}} - 3\)?
-
Cho khối lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a và mp (DBC’) hợp với mặt đáy (ABCD) một góc \({60^0}\). Tính theo a thể tích của khối lăng trụ ABCD.A’B’C’D’?
-
Đường thẳng nào là tiệm cận đứng của đồ thị hàm số sau \(y = \dfrac{2}{{ - x + 3}}\)?
-
Cho hình chóp S.ABC có đáy tam giác cân tại \(A\), mặt bên \(\left( {SBC} \right)\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(\left( {\alpha {\rm{\;}}} \right)\) là mặt phẳng đi qua điểm \(B\) và vuông góc với SC, chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó?
-
Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mp vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Biết \(AC = 2a,{\mkern 1mu} {\mkern 1mu} BD = 4a\). Tính theo \(a\) khoảng cách giữa 2 đường thẳng AD và SC?
-
Có tất cả bao nhiêu giá trị nguyên dương của \(m\) không vượt quá 2021 để phương trình \({4^{x - 1}} - m{.2^{x - 2}} + 1 = 0\) có nghiệm?
-
Trong không gian Oxyz, cho \(A\left( {1;1; - 1} \right),B\left( { - 1;2;0} \right),C\left( {3; - 1; - 2} \right)\). Giả sử \(M\left( {a;b;c} \right)\) thuộc mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = 861\) sao cho \(P = 2M{A^2} - 7M{B^2} + 4M{C^2}\) đạt giá trị nhỏ nhất. Giá trị \(T = \left| a \right| + \left| b \right| + \left| c \right|\) bằng?
-
Cho hình chóp \(S.ABCD\) có đáy hình chữ nhật, tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy, \(AB = a;\,\,AD = a\sqrt 3 \). Thể tích khối chóp S.ABCD bằng?
-
Có tất cả bao nhiêu cặp số nguyên dương \(\left( {x;y} \right)\) thỏa mãn \(x < y\) và \({4^x} + {4^y} = 32y - 32x + 48\)?
-
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng \(\sqrt 2 a\). Tam giác SAD cân tại \(S\) và mặt bên \(\left( {SAD} \right)\) vuông góc với mp đáy. Biết thể tích khối chóp S.ABCD bằng \(\dfrac{4}{3}{a^3}\). Tính khoảng cách h từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\)?
-
Làng gốm truyền thống Bát Tràng dự kiến làm 1 bức tranh gồm hình vuông cạnh \(4{\mkern 1mu} {\mkern 1mu} \left( m \right)\), thiết kế có 4 đường parabol chung đỉnh tại tâm của hình vuông, tạo nên bốn cánh hoa (tham khảo hình vẽ). Phần diện tích cánh hoa (phần tô đậm) sẽ được tráng một lớp men đặc biệt. Chi phí tráng lớp men đó có đơn giá là 24 triệu đồng/\({m^2}\). Tính số tiền phải trả để tráng men cho 4 cánh hoa?
-
Họ nguyên hàm của hàm số sau \(y = x\sin x\) là?
-
Cho bất phương trình sau \({\log _{\dfrac{1}{3}}}\left( {{x^2} - 2x + 6} \right) \le {\rm{\;}} - 2\). Mệnh đề nào đúng?
