Trắc nghiệm Số phức Toán Lớp 12

A. \(|w|=\sqrt{9-2 \sqrt{14}}\)

B. \(|w|=\sqrt{8-\sqrt{14}}\)

C. \(|w|=3 \sqrt{2}\)

D. \(|w|=3\)

A. \(|z|=5 \sqrt{2}\)

B. \(|z|=50\)

C. \(|z|=\frac{2 \sqrt{2}}{3}\)

D. \(|z|=5 \frac{10}{3}\)

A. \(|z|=\sqrt{5}\)

B. \(|z|=3\)

C. \(|z|=5\)

D. \(|z|=\sqrt{3}\)

A. \(|z|=\sqrt{10}\)

B. \(|z|=4\)

C. \(|z|=\frac{\sqrt{170}}{3}\)

D. \(|z|=10\)

A. |z|=7

B. |z|=25

C. \(|z|=\sqrt{7}\)

D. |z|=5

A. \(|z|=\sqrt{17}\)

B. \(|z|=10\)

C. \(|z|=17\)

D. \(|z|=\sqrt{10}\)

A. \(T=2^{1010}\)

B. \(T=2^{2019}\)

C. \(T=1\)

D. \(T=0\)

A. \(\frac{\sqrt{3}}{2}\)

B. \(2 \sqrt{3}\)

C. \(1\)

D. \(\sqrt 3\)

A. \(|z|=4 \sqrt{10}\)

B. \(|z|=4 \sqrt{5}\)

C. \(|z|=160\)

D. \(|z|=2 \sqrt{10}\)

A. \(|w|=\sqrt{130}\)

B. \(|w|=112\)

C. \(|w|=\sqrt{112}\)

D. \(|w|=130\)

A. \(\left|z_{1}+z_{2}\right|=-\sqrt{29}\)

B. \(\left|z_{1}+z_{2}\right|=\sqrt{29}\)

C. \(\left|z_{1}+z_{2}\right|=29\)

D. \(\left|z_{1}+z_{2}\right|=-29\)

A. \(|z|=\sqrt{7}\)

B. \(|z|=\sqrt{5}\)

C. \(|z|=\sqrt{15}\)

D. \(|z|=\sqrt{17}\)

A. \(|\bar{z}|=\sqrt{a+b}\)

B. \(|\bar{z}|=a^{2}+b^{2}\)

C. \(|\bar{z}|=\sqrt{a^{2}+b^{2}}\)

D. \(|\bar{z}|=\sqrt{a^{2}-b^{2}}\)

A. 4

B. 1

C. 2

D. 3

A. \(|z|=\sqrt{5}\)

B. \(|z|=\frac{5 \sqrt{5}}{2}\)

C. \(|z|=\frac{5 \sqrt{3}}{2}\)

D. \(|z|=5\)

A. \(\sqrt{\frac{85}{25}}\)

B. \(\frac{61}{5}\)

C. \(85\)

D. \(\sqrt{85}\)

A. \(|z|=4\)

B. \(|z|=\sqrt{17}\)

C. \(|z|=16\)

D. \(|z|=17\)

A. \(|w|=\sqrt{21}\)

B. \(|w|=\sqrt{15}\)

C. \(|w|=4\)

D. \(|w|=\sqrt{17}\)

A. \(3\)

B. \(\sqrt{3}\)

C. \(\sqrt{2}\)

D. \(2\)

A. \(\frac{\sqrt{91}}{3}\)

B. \(\frac{\sqrt{91}}{2}\)

C. \(\frac{\sqrt{61}}{2}\)

D. \(\frac{\sqrt{71}}{2}\)

A. \(z=2-3 i\)

B. \(z=6-3 i\)

C. \(z=-1-2 i\)

D. \(z=-1-4 i\)

A. \(\left(x-\frac{15}{8}\right)^{2}+\left(y-\frac{25}{8}\right)^{2}=\frac{9}{32}\)

B. \(\left(x+\frac{15}{8}\right)^{2}+\left(y+\frac{25}{8}\right)^{2}=\frac{9}{32}\)

C. \(\left(x+\frac{15}{8}\right)^{2}+\left(y-\frac{25}{8}\right)^{2}=\frac{9}{32}\)

D. \(\left(x-\frac{15}{8}\right)^{2}+\left(y+\frac{25}{8}\right)^{2}=\frac{9}{32}\)

A. \(z=1\)

B. \(z=-1\)

C. \(z=\sqrt{3}\)

D. \(z=1-\sqrt{3} i\)

A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0 ;-1) bán kính  \(R=\sqrt{3}\)

B. Tập hợp các điểm biểu diễn các số phức z là đường  tròn tâm I(0 ;-1) bán kính \(R=\sqrt{2}\)

C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0 ;1) bán kính  \(R=\sqrt{3}\)

D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2 ;-1)  bán kính  \(R=\sqrt{2}\)

A. \(2 \pi\)

B. \(\pi^{2}\)

C. \(\frac{\pi}{2}\)

D. \(\pi\)

A. Đường tròn tâm I(-2 ; 3) bán kính 1.

B. Đường tròn tâm I(-4 ; 1) bán kính 1.

C. Đường thẳng \(3 x+y-1=0\)

D. Đường thẳng \(3 x-y-1=0\)

A. đường tròn \(x^{2}+y^{2}=4\)

B. đường thẳng \(x-2 y-3=0\)

C. đường thẳng \(x+2 y+1=0\)

D. đường tròn \(x^{2}+y^{2}=2\)

A. Là một phần của đường thẳng \(y=3 x\)

B. Là một phần của đường thẳng \(y=\sqrt{3} x\)

C. Là một phần của đường thẳng \(y=-3 x\)

D. Là một phần của đường thẳng \(y=-\sqrt{3} x\)

A. \(d\left(d_{1}, d_{2}\right)=4\)

B. \(d\left(d_{1}, d_{2}\right)=1\)

C. \(d\left(d_{1}, d_{2}\right)=6\)

D. \(d\left(d_{1}, d_{2}\right)=2\)

A. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường thẳng.

B. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường tròn.

C. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường elip.

D. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là 2 điểm.

A. Parabol \(y^{2}=4 x\)

B. Đường thẳng \(6 x+8 y-25=0\)

C. Đường tròn \(x^{2}+y^{2}-4=0\)

D.  Elip \(\frac{x^{2}}{4}+\frac{y^{2}}{2}=1\)

A. Đường thẳng \(y=-\frac{1}{2}\)

B. Đường thẳng \(y=\frac{1}{2}\)

C. Đường tròn tâm I(0;1)

D. Đường thẳng y=2

A. \(3+i\)

B. \(1+3 i\)

C. \(2-3 i\)

D. \(-2+3 i\)

A. Hình chữ nhật giới hạn bởi các đường thẳng \(x=\pm 1 ; y=\pm 1\)

B. Trục Ox .

C. Đường tròn \((x+1)^{2}+(y-1)^{2}=1\)

D. Hai đường thẳng \(y=\pm 1\), trừ điểm

A. \(m=\frac{3}{2}\)

B. \(m=\frac{2}{3}\)

C. \(m=\frac{1}{2}\)

D. \(m=0\)

A. Đường tròn có phương trình \(\begin{array}{l} x^{2}+y^{2}=4 \end{array}\)

B.  Elip có phương trình \(x^{2}+4 y^{2}=4\)

C. Đường thẳng có phương trình \(x-2 y-3=0\)

D. Đường thẳng có phương trình \(x+2 y+1=0\)

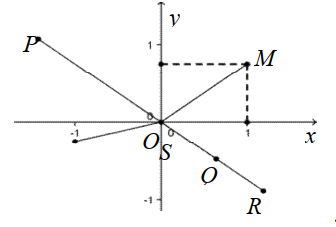
A. R

B. S

C. P

D. Q

A. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 4 .

B. Tập hợp điểm biểu diễn số phức z là một đường thẳng.

C. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 2 .

D. Tập hợp điểm biểu diễn số phức z là một đường Parabol.

A. Trục thực

B. Đường tròn trừ hai điểm trên trục ảo

C. Trục ảo trừ điểm (0;1)

D. Parabol

A. \(y=-x-1\)

B. \(y=x-1\)

C. \(y=x+1\)

D. \(y=-x+1\)

A. \(20 x-16 y-47=0\)

B. \(20 x+16 y+47=0\)

C. \(20 x+16 y-47=0\)

D. \(20 x-16 y+47=0\)

A. y=x+1

B. y=x

C. y=x-1

D. y=-x+1

A. Một đường thẳng có phương trình \(\begin{array}{l} 20 x-16 y-47=0 \end{array}\)

B. Một đường thẳng có phương trình \(3 y^{2}+20 x+2 y-20=0\)

C. Một đường thẳng có phương trình \( 20 x+16 y+47=0 \)

D. Một đường thẳng có phương trình \(-20 x+32 y+47=0\)

A. \(4 x+6 y-3=0\)

B. \(4 x+6 y+3=0\)

C. \(4 x-6 y+3=0\)

D. \(4 x-6 y-3=0\)

A. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường tròn.

B. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường elip.

C. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là 2 điểm.

D. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường thẳng.

A. \(T=36 \sqrt{2}\)

B. \(T=36 \sqrt{3}\)

C. \(T=18\)

D. \(T=24 \sqrt{3}\)

A. \(\left|z_{1}^{2}+z_{2}^{2}+z_{3}^{2}\right|=\left|z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1}\right|\)

B. \(\left|z_{1}^{2}+z_{2}^{2}+z_{3}^{2}\right|<\left|z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1}\right|\)

C. \(\left|z_{1}^{2}+z_{2}^{2}+z_{3}^{2}\right| \neq\left|z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1}\right|\)

D. \(\left|z_{1}^{2}+z_{2}^{2}+z_{3}^{2}\right|>\left|z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1}\right|\)

A. A(1 ; 3)

B. A(1 ;-3)

C. A(-1 ;-3)

D. A(-1 ; 3)

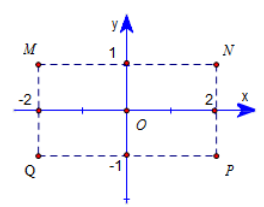
A. Điểm M

B. Điểm N

C. Điểm P

D. Điểm Q

A. (4 ; 6)

B. (-6 ;-4)

C. (-4 ;-6)

D. (4 ;-6)