Trắc nghiệm Số phức Toán Lớp 12
-
Câu 1:
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z tìm phần thực và phần ảo của số phức z .
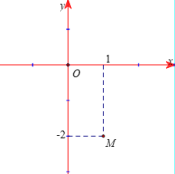
A. Phần thực là 1 và phần ảo là -2i
B. Phần thực là -2 và phần ảo là 1.
C. Phần thực là -2 và phần ảo là i .
D. Phần thực là 1 và phần ảo là -2 .
-
Câu 2:
Số phức z=2−3iz=2−3i có điểm biểu diễn trên mặt phẳng tọa độ là:
A. M(-2 ; 3)
B. M(2 ; 3)
C. M(-2 ;-3)
D. M(2 ;-3)
-
Câu 3:
Phần thực và phần ảo của các số phức 31+2i31+2i là:
A. 3535 và −65−65
B. 1515 và −25−25
C. 7575 và 6565
D. 1212 và 3
-
Câu 4:
Cho các số phức z thỏa mãn |z+1−i|=|z−1+2i||z+1−i|=|z−1+2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3 = 0
B. 4x-6y-3 = 0
C. 4x+6y+3 = 0
D. 4x-6y+3 = 0
-
Câu 5:
Cho số phức z = 2+i. Hãy xác định điểm biểu diễn hìnhhọc của số phức w = (1-i)z.
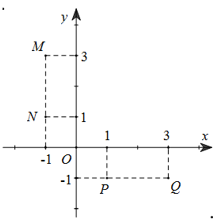
A. Điểm M
B. Điểm N
C. Điểm P
D. Điểm Q
-
Câu 6:
Cho A, B, C là các điểm biểu diễn các số phức thỏa mãn z3+i=0z3+i=0. Tìm phát biểu sai:
A. Tam giác ABC đều
B. Tam giác ABC có trọng tâm là O(0;0)
C. Tam giác ABC có tâm đường tròn ngoại tiếp là O(0;0)
D. SΔABC=3√34SΔABC=3√34
-
Câu 7:
Có bao nhiêu số phức z thỏa mãn: |z−i|=√2|z−i|=√2 và z2 là số thuần ảo
A. 3
B. 1
C. 4
D. 2
-
Câu 8:
Trên mặt phẳng phức, cho điểm A biểu diễn số phức 3-2i, điểm B biểu diễn số phức -1+6i. Gọi M là trung điểm của AB. Khi đó điểm M biểu diễn số phức nào trong các số phức sau:
A. 1-2i
B. 2-4i
C. 2+4i
D. 1+2i
-
Câu 9:
Cho số phức z thỏa mãn |6z−i2+3iz|≤1∣∣6z−i2+3iz∣∣≤1. Tìm giá trị lớn nhất của ∣∣z∣∣z.
A. max|z|=12max|z|=12
B. max|z|=34max|z|=34
C. max|z|=13max|z|=13
D. max|z|=1max|z|=1
-
Câu 10:
Cho số phức z thỏa mãn (2+3i)z−(1+2i)ˉz=7−i(2+3i)z−(1+2i)¯z=7−i. Tìm mô đun của z.
A. |z|=1|z|=1
B. |z|=2|z|=2
C. |z|=√3|z|=√3
D. |z|=√5|z|=√5
-
Câu 11:
Trong mặt phẳng tọa độ Oxy, cho điểm M là điểm biểu diễn của số phức z = 4+2i.
Phương trình đường trung trực của đoạn OM là:
A. x+2y+5 = 0
B. x+2y-5 = 0
C. x-2y+5 = 0
D. 2x+y+5 = 0
-
Câu 12:
Gọi P là điểm biểu diễn của số phức a+bi trong mặt phẳng phức.
Cho các mệnh đề sau:
(1) Môđun của a+bi là bình phương khoảng cách OP.
(2) Nếu P là biểu diễn của số 3+4i thì khoảng cách từ O đến P bằng 7.
Chọn đáp án đúng:
A. Chỉ có (1) đúng
B. Chỉ có (2) đúng
C. Cả hai đều đúng
D. Cả hai đều sai
-
Câu 13:
Trong mặt phẳng tọa độ Oxy, cho ba điểm M,N,P là điểm biểu diễn của 3 số phức:z1=8+3i;z2=1+4i;z3=5+xiz1=8+3i;z2=1+4i;z3=5+xi. Với giá trị nào của x thì tam giác MNP vuông tại P?
A. 1 và 2
B. 0 và 7
C. -1 và -7
D. 3 và 5
-
Câu 14:
Cho số phức z biết z+2ˉz=(1−i√2)(1+i)22−iz+2¯z=(1−i√2)(1+i)22−i (1)
Tìm tổng phần thực và phần ảo của z
A. 4√2−2154√2−215
B. −2√2−45−2√2−45
C. −2√2−1415−2√2−1415
D. −2√2−145−2√2−145
-
Câu 15:
Cho số phức z thỏa mãn: (2+i)z+2(1+2i)1+i=7+8i(2+i)z+2(1+2i)1+i=7+8i (1)
Chọn đáp án sai?
A. z là số thuần ảo
B. z có phần ảo là số nguyên tố
C. z có phần thực là số nguyên tố
D. z có tổng phần thực và phần ảo là 5
-
Câu 16:
Cho số phức z thỏa mãn z=(3i+4)[(−3+2i)−(4−7i)]z=(3i+4)[(−3+2i)−(4−7i)]
Tính tích phần thực và phần ảo của z.¯zz.¯¯¯z
A. 30
B. 3250
C. 70
D. 0
-
Câu 17:
Cho số phức z = x+yi với x, y là các số thực không âm thỏa mãn |z−3z−1+2i|=1∣∣z−3z−1+2i∣∣=1 và biểu thức P=|z2−z−2|+i(z2−z−2)[z(1−i)+ˉz(1+i)]P=∣∣z2−z−2∣∣+i(z2−z−2)[z(1−i)+¯z(1+i)]. Giá trị lớn nhất và giá trị nhỏ nhất của P lần lượt là:
A. 0 và -1
B. 3 và -1
C. 3 và 0
D. 2 và 0
-
Câu 18:
Trong mặt phẳng Oxy, M,N,P là tọa độ điểm biểu diễn của số phức z1=−5+6i;z2=−4−i;z3=4+3iz1=−5+6i;z2=−4−i;z3=4+3i
Tọa độ trực tâm H của tam giác MNP là:
A. (3;1)
B. (-1;3)
C. (2;-3)
D. (-3;2)
-
Câu 19:
Cho các số phức z1=1;z2=2+2i;z3=−1+3i được biểu diễn trong mặt phẳng tọa độ Oxy là M,N,P, các điểm này lần lượt là trung điểm của ba cạnh tam giác EFH. Tọa độ trọng tâm G của tam giác EFH là:
A. (2;3)
B. (3;2)
C. (23;23)
D. (23;53)
-
Câu 20:
Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=|z−3−3i|
Tính M.m
A. M.m = 25
B. M.m = 20
C. M.m = 30
D. M.m = 24
-
Câu 21:
Gọi T là tập hợp các số phức z thỏa mãn |z−i|≥3 và |z−1|≤5. Gọi z1,z2∈T lần lượt là các số phức có môdun nhỏ nhất và lớn nhất. Tìm số phức z1+2z2
A. 12+2i
B. -2+12i
C. 6-4i
D. 12+4i
-
Câu 22:
Trên mặt phẳng tọa độ Oxy. Cho tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |−2+i(z−1)|=5. Phát biểu nào sau đây là sai:
A. Tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(1; –2)
B. Tập hợp điểm biểu diễn các số phức z là đường tròn có bán kính R = 5
C. Tập hợp điểm biểu diễn các số phức z là đường tròn có đường kính bằng 10
D. Tập hợp điểm biểu diễn các số phức z là hình tròn có bán kính R = 5
-
Câu 23:
Số phức z = -4+3i được biểu diễn bởi điểm M có tọa độ
A. M(4;-3)
B. M(-4;3)
C. M(3;-4)
D. M(4;3)
-
Câu 24:
Tìm phần thực của số phức z21+z22 biết rằng z1, z2 là hai nghiệm phức của phương trình z2−4z+5 = 0
A. 4
B. 6
C. 8
D. 5
-
Câu 25:
Điểm M trong hình bên là điểm biểu diễn của số phức z. Mệnh đề nào dưới đây đúng?
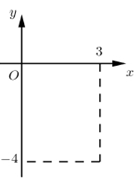
A. Phần thực là 3 và phần ảo là -4.
B. Phần thực là -4 và phần ảo là 3i.
C. Phần thực là -4 và phần ảo là 3.
D. Phần thực là 3 và phần ảo là -4i.
-
Câu 26:
Nghiệm phức có phần ảo dương của phương trình z2−z+1=0 là z=a+bi,a,b∈R. Tính a+√3b
A. 2
B. 1
C. - 2
D. - 1
-
Câu 27:
Tìm tọa độ điểm biểu diễn của số phức z=(2−3i)(4−i)3+2i
A. (-1;-4)
B. (1;4)
C. (1;-4)
D. (-1;4)
-
Câu 28:
Trong các số phức: (1+i)2,(1+i)8,(1+i)3,(1+i)5 số phức nào là số thực?
A. (1+i)3
B. (1+i)8
C. (1+i)2
D. (1+i)5
-
Câu 29:
Số phức z thỏa mãn |z|=5 và số phức w=(1+i)ˉz. Tìm |w|
A. √10
B. √2+√5
C. 5
D. 2√5
-
Câu 30:
Cho số phức z = (1+2i)(5-i), z có phần thực là
A. 5
B. 7
C. 3
D. 9
-
Câu 31:
Cho số phức z = -3+4i. Môđun của z là
A. 4
B. 7
C. 3
D. 5
-
Câu 32:
Cho số phức z có biểu diễn hình học là điểm M ở hình vẽ bên. Khẳng định nào sau đây đúng ?
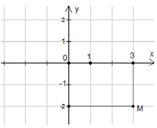
A. z = -3+2i
B. z = 3+2i
C. z = -3-2i
D. z = 3-2i
-
Câu 33:
Cho số phức z thỏa mãn z+4ˉz=7+i(z−7). Khi đó, môđun của z bằng bao nhiêu
A. |z|=5
B. |z|=√3
C. |z|=√5
D. |z|=3
-
Câu 34:
Cho hai số phức z1 = 2+3i và z2 = −3−5i
Tính tổng phần thực và phần ảo của số phức w = z1+z2
A. 3
B. 0
C. - 1 - 2i
D. - 3
-
Câu 35:
Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức (z−ˉz)2 với z=a+bi(a,b∈R,b≠0)
Chọn kết luận đúng
A. M thuộc tia Ox.
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox.
D. M thuộc tia đối của tia Oy.
-
Câu 36:
Cho số phức z thỏa mãn z(2-i)+13i = 1. Tính mô đun của số phức z.
A. |z|=34
B. |z|=√34
C. |z|=√343
D. |z|=5√343
-
Câu 37:
Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức z=(1+i)(2−i)?
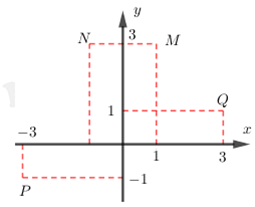
A. P
B. M
C. N
D. O
-
Câu 38:
Trong mặt phẳng Oxy, cho các điểm A, B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức
A. -1+2i
B. −12+2i
C. 2 - i
D. 2−12i
-
Câu 39:
Cho số phức z=(1+i)2(1+2i). Số phức z có phần ảo là
A. 2
B. 4
C. - 2
D. 2i
-
Câu 40:
Có bao nhiêu số phức z thỏa mãn đồng thời hai điều kiện sau: |z−10+2i|=|z+2−14i| và |z−1−10i|=5?
A. Vô số
B. Một
C. Không
D. Hai
-
Câu 41:
Có bao nhiêu số phức thỏa mãn z+|z|2.i−1−34i=0
A. 1
B. 3
C. 2
D. 0
-
Câu 42:
Cho biết có hai số phức z thỏa mãn z2 = 119−120i, kí hiệu là z1 và z2.
Tính |z1−z2|2
A. 169
B. 114244
C. 338
D. 676
-
Câu 43:
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z.
Tính |z| biết diện tích tam giác OAB bằng 8.
A. |z|=2√2
B. |z|=4√2
C. |z|=2
D. |z|=4
-
Câu 44:
Gọi z1 là nghiệm phức có phần ảo âm của phương trình z2−2z+5 = 0
Tìm tọa độ điểm biểu diễn cho số phức 7−4iz1 trong mặt phẳng phức?
A. P(3;2)
B. N(1;2)
C. Q(3;-2)
D. M(1;2)
-
Câu 45:
Cho số phức z thỏa mãn z(1−2i)+ˉzi=15+i
Tìm môđun của số phức z.
A. |z|=5
B. |z|=4
C. |z|=2√5
D. |z|=2√3
-
Câu 46:
Cho số phức z thỏa mãn z(2−i)+13i=1. Tính môđun của số phức z
A. |z|=34
B. |z|=5√343
C. |z|=√343
D. |z|=√34
-
Câu 47:
Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức ˉz là:
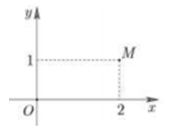
A. 2 - i
B. 1+2i
C. 1 - 2i
D. 2 + i
-
Câu 48:
Cho hai số phức z1=−1+2i,z2=−1−2i
Giá trị của biểu thức |z1|2+|z2|2 bằng
A. √10
B. 10
C. - 6
D. 4
-
Câu 49:
Tìm phần ảo của số phức z, biết (1+i)z = 3-i
A. 2
B. - 2
C. 1
D. - 1
-
Câu 50:
Cho z là các số phức thỏa mãn điều kiện |z+31−2i+2|=1 và w là số thuần ảo.
Giá trị nhỏ nhất của biểu thức |z−w| bằng
A. 5−√5
B. √5
C. 2√2
D. 1+√3














