Trắc nghiệm Số phức Toán Lớp 12
-
Câu 1:
Cho số phức \(\bar{z}=(1+2 i)(4-3 i)\) . Tọa độ điểm biểu diễn số phức z trên mặt phẳng phức là:
A. (10 ;-5)
B. (-10 ;-5)
C. (10 ; 5)
D. (-10 ; 5)
-
Câu 2:
Trong mặt phẳng phức, tìm điểm M biểu diễn số phức \(z=\frac{i^{2017}}{3+4 i}\)
A. \(M\left(\frac{4}{25} ;-\frac{3}{25}\right)\)
B. \(M\left(\frac{4}{25} ; \frac{3}{25}\right)\)
C. \(M\left(-\frac{4}{25} ;-\frac{3}{25}\right)\)
D. \(M\left(-\frac{4}{25} ; \frac{3}{25}\right)\)
-
Câu 3:
Trong mặt phẳng Oxy, cho \(z_{1}=1-i, z_{2}=3+2 i\) , gọi các điểm M , N lần lượt là điểm biểu diễn số phức \(z_{1}, z_{2}\) , gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
A. \(\frac{4}{3}+\frac{1}{3} i\)
B. \(2+\frac{1}{2} i\)
C. \(5-i\)
D. \(4+i\)
-
Câu 4:
Cho hình vuông ABCD có tâm H và A, B, C, D, H lần lượt là điểm biểu diễn cho các số phức a , b , c, d , h . Biết \(a=-2+i, h=1+3 i\) và số phức b có phần ảo dương. Khi đó, mô- đun của số phức b là
A. \(\sqrt{37} .\)
B. \(\sqrt{13} .\)
C. \(\sqrt{26}\)
D. \(\sqrt{10}\)
-
Câu 5:
Cho hai số phức z , w thỏa mãn \(|z+2 w|=3,|2 z+3 w|=6 \text { và }|z+4 w|=7\) . Tính giá trị của biểu thức \(P=z \cdot \bar{w}+\bar{z} \cdot w\)
A. P=-14
B. P=-28
C. P=-14i
D. P=-28 i
-
Câu 6:
Cho số phức z thỏa mãn điều kiện \(z+(i-2) z=2+3 i\). Điểm M là điểm biểu diễn số phức z trên mặt phẳng tọa độ Oxy . Tọa độ của điểm M là
A. \(M\left(-\frac{1}{2} ; \frac{5}{2}\right)\)
B. \(M\left(\frac{1}{2} ;-\frac{5}{2}\right)\)
C. \(M\left(\frac{1}{2} ; \frac{5}{2}\right)\)
D. \(M\left(-\frac{1}{2} ;-\frac{5}{2}\right)\)
-
Câu 7:
Kí hiệu z0 là nghiệm phức có phần ảo dương của phương trình \(4 z^{2}-16 z+17=0\) . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức \(w=i_{20} ?\)
A. \(M_{1}\left(\frac{1}{2} ; 2\right)\)
B. \(M_{4}\left(\frac{1}{4} ; 1\right)\)
C. \(M_{3}\left(-\frac{1}{4} ; 1\right)\)
D. \(M_{2}\left(-\frac{1}{2} ; 2\right)\)
-
Câu 8:
Điểm biểu diễn của số phức z thỏa \((1+i) z=(1-2 i)^{2}\)
A. \(\left(-\frac{7}{2} ;-\frac{1}{2}\right)\)
B. \(\left(\frac{7}{2} ; \frac{1}{2}\right)\)
C. \(\left(\frac{7}{2} ;-\frac{1}{2}\right)\)
D. \(\left(-\frac{7}{2} ; \frac{1}{2}\right)\)
-
Câu 9:
Cho số phức z thỏa \((1+i)=14-2 i\) . Điểm biểu diễn của số phức z trong mặt phẳng tọa độ Oxy có tọa độ là:
A. (8 ; 6)
B. (6 ; 8)
C. (6 ;-8)
D. (-8 ; 6)
-
Câu 10:
Cho số phức z thoả mãn \((2-i) z=1+i\)Điểm M biểu diễn số phức z trên mặt phẳng toạ độ Oxy là
A. \(\left(\frac{3}{4} ; 0\right)\)
B. \(M\left(-\frac{1}{5} ; \frac{3}{5}\right)\)
C. \(M\left(\frac{1}{5} ; \frac{3}{5}\right)\)
D. \(M\left(0 ; \frac{3}{5}\right)\)
-
Câu 11:
Cho số phức \(z_{1}, z_{2}, z_{3}\) thỏa mãn \(\left|z_{1}\right|=\left|z_{2}\right|=\left|z_{3}\right|=1 \text { và } z_{1}+z_{2}+z_{3}=0\) . Tính \(z_{1}^{2}+z_{2}^{2}+z_{3}^{2}\)
A. A=1
B. A=-1
C. A=0
D. A=1+i
-
Câu 12:
Gọi A, B, C lần lượt là các điểm biểu diễn của các số phức \(z_{1}=2, z_{2}=4 i, z_{3}=2+4 i\) trong mặt phẳng tọa độ Oxy. Tính diện tích tam giác ABC
A. 6
B. 4
C. 8
D. 2
-
Câu 13:
Số nào sau đây là số đối của số phức z , biết z có phần thực dương thỏa mãn \(|z|=2\) và trong mặt phẳng phức thì z có điểm biểu diễn thuộc đường thẳng \(y-\sqrt{3} x=0\)
A. \(1+\sqrt{3} i\)
B. \(-1-\sqrt{3} i\)
C. \(-1+\sqrt{3} i\)
D. \(1-\sqrt{3} i\)
-
Câu 14:
Cho hai số phức \(z_{1}=1-3 i, z_{2}=-4-6 i\) có các điểm biểu diễn trên mặt phẳng tọa độ lần lượt là hai điểm M và N . Gọi z là số phức mà có điểm biểu diễn là trung điểm của đoạn MN. Hỏi z là số phức nào trong các số phức dưới đây?
A. \(z=\frac{5}{2}+\frac{3}{2} i\)
B. \(z=-\frac{3}{2}-\frac{9}{2} i\)
C. \(z=-3-9 i\)
D. \(z=-1-3 i\)
-
Câu 15:
Cho số phức z thỏa mãn \(i z+2-i=0\) . Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A. \(\sqrt{13}\)
B. \(2 \sqrt{10}\)
C. \(2 \sqrt{2}\)
D. \(2 \sqrt{5}\)
-
Câu 16:
Cho 3 điểm A , B , C lần lượt biểu diễn cho các số phức \(z_{1}, z_{2}, z_{3}\) . Biết \(\left|z_{1}\right|=\left|z_{2}\right|=\left|z_{3}\right|\) và \({z_{1}}+z_{2}=0\) . Khi đó tam giác ABC là tam giác gì?
A. Tam giác ABC đều.
B. Tam giác ABC vuông tại C .
C. Tam giác ABC cân tại C .
D. Tam giác ABC vuông cân tại C
-
Câu 17:
Gọi điểm A B , lần lượt biểu diễn các số phức \(z_{1} ; z_{2} ;\left(z_{1} \cdot z_{2} \neq 0\right)\) trên mặt phẳng tọa độ ( \(A, B, C \text { và } A^{\prime}, B^{\prime}, C^{\prime}\) đều không thẳng hàng) và \(z_{1}^{2}+z_{2}^{2}=z_{1} \cdot z_{2}\) . Với O là gốc tọa độ, khẳng định nào sau đây đúng?
A. Tam giác OAB vuông cân tại B.
B. Diện tích tam giác OAB không đổi.
C. Tam giác OAB đều.
D. Tam giác OAB vuông cân tại O
-
Câu 18:
Cho số phức z thỏa mãn \((1-2 i)=3+i\). Hỏi điểm biểu diễn của z là điểm nào trong các điểm I, J, K, H ở hình bên?
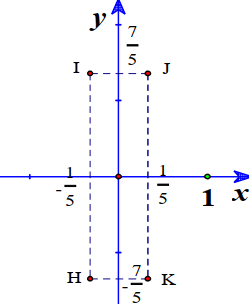
A. Điểm H
B. Điểm I
C. Điểm J
D. Điểm K
-
Câu 19:
Cho số phức \(z=(1+i)^{8}\) . Tọa độ điểm M biểu diễn z là.
A. M(16 ; 0)
B. M(-16 ; 0)
C. M(0 ; 16)
D. M(0 ;-16)
-
Câu 20:
Cho số phức z thỏa mãn \(|z-2+3 i|=|z-2-3 i|\). Biết \(|z-1-2 i|+|z-7-4 i|=6 \sqrt{2}, M(x ; y)\) là điểm biểu diễn số phức z , khi đó x thuộc khoảng
A. (1 ; 3)
B. (4 ; 8)
C. (2 ; 4)
D. (0 ; 2)
-
Câu 21:
Mặt phẳng phức \(A(-4 ; 1), B(1 ; 3), C(-6 ; 0)\) lần lượt biểu diễn các số phức \(z_{1}, z_{2}, z_{3}\). Trọng tâm G của tam giác ABC biểu diễn số phức nào sau đây?
A. \(3+\frac{4}{3} i\)
B. \(-3-\frac{4}{3} i\)
C. \(-3+\frac{4}{3} i\)
D. \(3-\frac{4}{3} i\)
-
Câu 22:
Kí hiệu z1 là nghiệm phức có phần ảo âm của phương trình \(6 z^{2}-12 z+7=0\) . Trên mặt phẳng tọa độ, tìm điểm biểu diễn của số phức \(w=i z_{1}-\frac{1}{\sqrt{6}}\)
A. (0 ; 1)
B. (1 ; 0)
C. (0 ;-1)
D. (1 ; 1)
-
Câu 23:
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm môđun của số phức z .
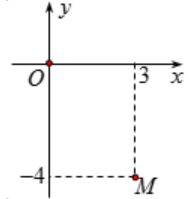
A. \(|z|=5\)
B. \(|z|=3\)
C. \(|z|=-4\)
D. \(|z|=4\)
-
Câu 24:
Cho các số phức \(z_{1}, z_{2}, z_{3}, z_{4}\)có các điểm biểu diễn trên mặt phẳng phức lần lượt là A, B, C, D (như hình bên). Tính \(P=\left|z_{1}+z_{2}+z_{3}+z_{4}\right|\)
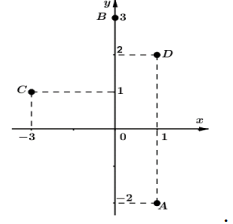
A. \(P=3\)
B. \(P=\sqrt{5}\)
C. \(P=2\)
D. \(P=\sqrt{17}\)
-
Câu 25:
Kí hiệu A , B , C lần lượt là các điểm biểu diễn hình học của các số phức \(z_{1}=1+i ; z_{2}=(1+i)^{2}, z_{3}=a-i, a \in \mathbb{R}\) . Tìm a để tam giác ABC vuông tại B
A. a=1
B. a=3
C. a=-1
D. a=-3
-
Câu 26:
Cho hai điểm A , B là hai điểm biểu diễn hình học số phức theo thứ tự \(z_{0}, z_{1}\) khác 0 và thỏa mãn đẳng thức \(z_{0}^{2}+z_{1}^{2}=z_{0} z_{1}\) . Hỏi ba điểm O , A , B tạo thành tam giác gì? ( O là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
A. Vuông tại O .
B. Cân tại O
C. Vuông cân tại O .
D. Đều.
-
Câu 27:
Điểm biểu diễn số phức \(z=\frac{(2-3 i)(4-i)}{3+2 i}\) có tọa độ là
A. (1 ; 4)
B. (1 ;-4)
C. (-1 ;-4)
D. (-1 ; 4)
-
Câu 28:
Cho số phức z thỏa mãn \((1+i) z=11-3 i\) . Điểm M biểu diễn cho số phức z trong mặt phẳng tọa độ là
A. M(7 ;-7)
B. M(4 ;-7)
C. M(14 ;-14)
D. M(8 ;-14)
-
Câu 29:
Điểm M trong hình bên là điểm biểu diễn cho số phức
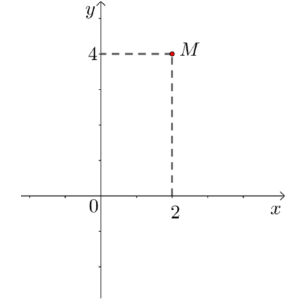
A. \(z=2-4 i\)
B. \(z=4-2 i\)
C. \(z=2+4 i\)
D. \(z=4+2 i\)
-
Câu 30:
Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình \((1+i) \bar{z}=3-5 i\)
A. M(1 ;-4)
B. M(-1 ;-4)
C. M(1 ; 4)
D. M(-1 ; 4)
-
Câu 31:
Cho số phức \(z=1-2i\) . Tìm tọa độ biểu diễn của số phức \(\bar z\) trên mặt phẳng tọa độ
A. M(2 ;-1)
B. M(1 ; 2)
C. M(1 ;-2)
D. M(2 ; 1)
-
Câu 32:
Tọa độ điểm biểu diễn hai số phức z và z' lần lượt là tọa độ của hai vectơ \(\vec{u} \text { và } \vec{u}^{\prime}\) . Hãy chọn câu trả lời sai trong các câu sau:
A. Nếu \(z=a+b i \text { thì } \vec{u}=\overrightarrow {O M}, \text { với } M(a ; b)\)
B. \(\vec{u}-\vec{u}^{\prime}\) biểu diễn cho số phức \(z-z^{\prime}\)
C. \(\vec{u}.\vec{u}^{\prime}\) biểu diễn cho số phức \(z.z^{\prime}\)
D. \(\vec{u}+\vec{u}^{\prime}\) biểu diễn cho số phức \(z+z^{\prime}\)
-
Câu 33:
Tìm điểm biểu diễn của số phức \(z=\frac{1}{2-3 i}\) trong mặt phẳng tọa độ Oxy?
A. \(\left(\frac{2}{13} ; \frac{3}{13}\right)\)
B. \(\left(\frac{-2}{13} ; \frac{3}{13}\right)\)
C. \(\left(\frac{-2}{13} ; \frac{-3}{13}\right)\)
D. \(\left(\frac{2}{13} ; \frac{-3}{13}\right)\)
-
Câu 34:
Điểm biểu diễn của số phức z là M (1;2). Tọa độ của điểm biểu diễn cho số phức \(w=z-2 \bar{z}\) là
A. (2 ; 1)
B. (-1 ; 6)
C. (2 ; 3)
D. (2 ;-3)
-
Câu 35:
Điểm M trong hình vẽ trên là điểm biểu diễn cho số phức z. Phần ảo của số phức \((1+i)z\) bằng?
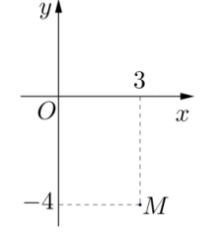
A. -7
B. 1
C. -1
D. 7
-
Câu 36:
Gọi M , M' theo thứ tự là các điểm biểu diễn số phức \(z \neq 0 \text { và } z^{\prime}=\frac{1+i}{2} z\) . Trong các khẳng định sau, khẳng định nào là đúng?
A. \(\Delta O M M^{\prime}\) là tam giác đều.
B. \(\Delta O M M^{\prime}\) là tam giác tù
C. \(\Delta O M M^{\prime}\) là tam giác vuông cân
D. \(\Delta O M M^{\prime}\) là tam giác nhọn.
-
Câu 37:
Cho số phức z thỏa mãn điều kiện \(z-(2+3 i) \bar{z}=1-9 i\) . Số phức \(w=\frac{5}{i z}\) có điểm biểu diễn là điểm nào trong các điểm A , B , C , D ở hình bên?

A. Điểm B
B. Điểm D
C. `Điểm A
D. Điểm C
-
Câu 38:
Cho số phức z thỏa mãn \((1-i) z=2 i\) . Tìm điểm biểu diễn của z trên mặt phẳng tọa độ (Oxy)
A. \(M(-1 ; 1)\)
B. \(Q(-1 ;-1)\)
C. \(P(1 ;-1)\)
D. \(N(1 ; 1)\)
-
Câu 39:
Cho tam giác ABC có ba đỉnh A , B , C lần lượt là điểm biểu diễn hình học của các số phức \(z_{1}=2-i, z_{2}=-1+6 i, z_{3}=8+i\) . Số phức z4 có điểm biểu diễn hình học là trọng tâm của tam giác ABC . Mệnh đề nào sau đây là đúng
A. \(\left(z_{4}\right)^{2}=13+12 i\)
B. \(\bar{z}_{4}=3-2 i\)
C. \(z_{4}=3-2 i\)
D. \(\left|z_{4}\right|=5\)
-
Câu 40:
Gọi z1 là nghiệm phức có phần ảo dương của phương trình \(z^{2}+6 z+13=0\) . Tìm tọa độ điểm M biểu diễn số phức \(w=(i+1) z_{1}\)
A. \(M(1 ; 5)\)
B. \(M(-5 ;-1)\)
C. \(M(5 ; 1)\)
D. \(M(-1 ;-5)\)
-
Câu 41:
Cho A , B , C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức \(z_{1}=1+2 i, z_{2}=-2+5 i, z_{3}=2+4 i\),. Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
A. \(1+5 i\)
B. \(3+5 i\)
C. \(-1+7 i\)
D. \(5+i\)
-
Câu 42:
Giả sử A , B theo thứ tự là điểm biểu diễn của các số phức \(z_1 ; z_2\) . Khi đó độ dài của véctơ\(\overrightarrow {A B}\) bằng:
A. \(\left|z_{1}\right|-\left|z_{2}\right|\)
B. \(\left|z_{2}-z_{1}\right|\)
C. \(\left|z_{1}\right|+\left|z_{2}\right|\)
D. \(\left|z_{2}+z_{1}\right|\)
-
Câu 43:
Biết số phức z có điểm biểu diễn trên mặt phẳng tọa độ là A(1; -2) .Tìm số phức z
A. \(z=2-i\)
B. \(z=1-2 i\)
C. \(z=-2+i\)
D. \(z=-1+2 i\)
-
Câu 44:
Điểm biểu diễn hình học của số phức \(z=\frac{25}{3+4 i}\) là:
A. (2 ;-3)
B. (3 ;-2)
C. (3 ;-4)
D. (3 ; 4)
-
Câu 45:
Cho số phức z=-4+2 i . Trong mặt phẳng phức, điểm biểu diễn của z có tọa độ là.
A. \(M(-4 i ; 2)\)
B. \(M(-4 ; 2 i)\)
C. \(z=-4+2 i\)
D. \(M(2 ;-4)\)
-
Câu 46:
Cho số phức \(z=-2+i\) . Điểm nào dưới đây là điểm biểu diễn của số phức \(w=i z\) trên mặt phẳng tọa độ ?
A. M(-1 ;-2)
B. N(2 ; 1)
C. Q(1 ; 2)
D. P(-2 ; 1)
-
Câu 47:
Cho số phức z thỏa mãn \((1+3 i) z+2 i=-4\) . Điểm nào sau đây biểu diễn cho z trong các điểm M , N , P , Q ở hình bên.
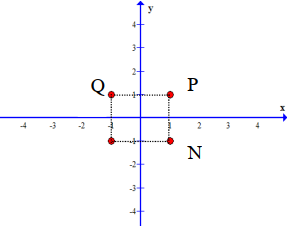
A. Điểm M
B. Điểm N
C. Điểm P
D. Điểm Q
-
Câu 48:
Cho số phức z thỏa mãn \((4-i) z=3-4 i\). Điểm biểu diễn của z là
A. \(M\left(\frac{16}{15} ;-\frac{11}{15}\right)\)
B. \(M\left(\frac{9}{5} ;-\frac{4}{5}\right)\)
C. \(M\left(\frac{9}{25} ;-\frac{23}{25}\right)\)
D. \(M\left(\frac{16}{17} ;-\frac{13}{17}\right)\)
-
Câu 49:
Tìm điểm M biểu diễn số phức \(z=i-2\)
A. M(4 ; 3)
B. M(-3 ; 4)
C. M(3 ; 4)
D. M(4 ;-3)
-
Câu 50:
Cho số phức \(z=2018-2017 i\). Điểm M biểu diễn của số phức liên hợp của z là
A. \(M(2018 ; 2017)\)
B. \(M(2018 ;-2017)\)
C. \(M(-2018 ;-2017)\)
D. \(M(-2018 ; 2017)\)














