ADMICRO
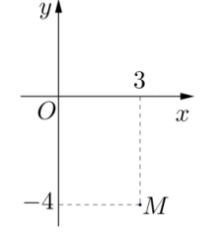
Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức với
Chọn kết luận đúng
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo saiTa có
Do
Do đó M có phần thực âm, phần ảo bằng 0, nên thuộc tia đối của tia Ox.
ZUNIA9
AANETWORK