Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán Lớp 12
-
Câu 1:
Cho hàm số y=f(x) có bảng biến thiên như hĩnh vẽ.
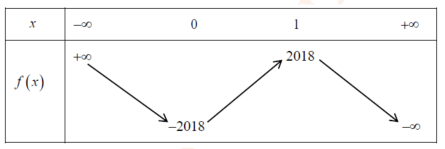
Hỏi phương trình \(|f(x+2017)-2018|=2019\) có bao nhiêu nghiệm?
A. 6
B. 2
C. 4
D. 3
-
Câu 2:
Cho hàm của hàm số f(x) đồng biến trên tập số thực R, mệnh đề nào sau đây là đúng ?
A. Với mọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaGaamiEamaaBa % aaleaacaaIXaaabeaakiaacYcacaWG4bWaaSbaaSqaaiaaikdaaeqa % aOGaeyicI4SaeSyhHeQaaeiiaiabgkDiElaadAgadaqadaqaaiaadI % hadaWgaaWcbaGaaGymaaqabaaakiaawIcacaGLPaaacqGH8aapcaWG % MbWaaeWaaeaacaWG4bWaaSbaaSqaaiaaikdaaeqaaaGccaGLOaGaay % zkaaaaaa!49AC! {x_1},{x_2} \in R{\rm{ }} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
B. Với mọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaGaamiEamaaBa % aaleaacaaIXaaabeaakiabgYda8iaadIhadaWgaaWcbaGaaGOmaaqa % baGccqGHiiIZcqWIDesOcaqGGaGaeyO0H4TaamOzamaabmaabaGaam % iEamaaBaaaleaacaaIXaaabeaaaOGaayjkaiaawMcaaiabgYda8iaa % dAgadaqadaqaaiaadIhadaWgaaWcbaGaaGOmaaqabaaakiaawIcaca % GLPaaaaaa!4A00! {x_1} < {x_2} \in R {\rm{ }} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
C. Với mọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaGaamiEamaaBa % aaleaacaaIXaaabeaakiaacYcacaWG4bWaaSbaaSqaaiaaikdaaeqa % aOGaeyicI4SaeSyhHeQaaeiiaiabgkDiElaadAgadaqadaqaaiaadI % hadaWgaaWcbaGaaGymaaqabaaakiaawIcacaGLPaaacqGH+aGpcaWG % MbWaaeWaaeaacaWG4bWaaSbaaSqaaiaaikdaaeqaaaGccaGLOaGaay % zkaaaaaa!49B0! {x_1},{x_2} \in R {\rm{ }} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
D. Với mọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaGaamiEamaaBa % aaleaacaaIXaaabeaakiabg6da+iaadIhadaWgaaWcbaGaaGOmaaqa % baGccqGHiiIZcqWIDesOcaqGGaGaeyO0H4TaamOzamaabmaabaGaam % iEamaaBaaaleaacaaIXaaabeaaaOGaayjkaiaawMcaaiabgYda8iaa % dAgadaqadaqaaiaadIhadaWgaaWcbaGaaGOmaaqabaaakiaawIcaca % GLPaaaaaa!4A04! {x_1} > {x_2} \in R{\rm{ }} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
-
Câu 3:
Phát biểu nào sau đây là đúng?
A. Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGacaGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyyzImRaaGimaiaaykW7 % caaMc8UaeyiaIiIaamiEaiabgIGiopaabmaabaGaamyyaiaacUdaca % WGIbaacaGLOaGaayzkaaaaaa!466B! f'\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right)\) thì hàm số y = f(x) đồng biến trên (a;b).
B. Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGacaGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyOpa4JaaGimaiaaykW7 % caaMc8UaeyiaIiIaamiEaiabgIGiopaabmaabaGaamyyaiaacUdaca % WGIbaacaGLOaGaayzkaaaaaa!45AD! f'\left( x \right) > 0\,\,\forall x \in \left( {a;b} \right)\) thì hàm số y = f(x) đồng biến trên (a,b).
C. Hàm số y = f(x) đồng biến trên (a,b) khi và chỉ khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGacaGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyyzImRaaGimaiaaykW7 % caaMc8UaeyiaIiIaamiEaiabgIGiopaabmaabaGaamyyaiaacUdaca % WGIbaacaGLOaGaayzkaaaaaa!466B! f'\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right)\) .
D. Hàm số y = f(x) đồng biến trên (a,b) khi và chỉ khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGacaGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyOpa4JaaGimaiaaykW7 % caaMc8UaeyiaIiIaamiEaiabgIGiopaabmaabaGaamyyaiaacUdaca % WGIbaacaGLOaGaayzkaaaaaa!45AD! f'\left( x \right) > 0\,\,\forall x \in \left( {a;b} \right)\)
-
Câu 4:
Cho hàm số y = f(x) có đạo hàm trên (a;b) . Phát biểu nào sau đây là đúng ?
A. Hàm số f(x) đồng biến trên (a;b) khi và chỉ khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyyzImRaaGimaiaacYca % cqGHaiIicaWG4bGaeyicI48aaeWaaeaacaWGHbGaai4oaiaadkgaai % aawIcacaGLPaaaaaa!4407! f'\left( x \right) \ge 0,\forall x \in \left( {a;b} \right)\)
B. Hàm số f(x) đồng biến trên (a;b) khi và chỉ khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyipaWJaaGimaiaacYca % cqGHaiIicaWG4bGaeyicI48aaeWaaeaacaWGHbGaai4oaiaadkgaai % aawIcacaGLPaaaaaa!4345! f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)\)
C. Hàm số f(x) đồng biến trên (a;b) khi và chỉ khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaiaacYca % cqGHaiIicaWG4bGaeyicI48aaeWaaeaacaWGHbGaai4oaiaadkgaai % aawIcacaGLPaaaaaa!43F6! f'\left( x \right) \le 0,\forall x \in \left( {a;b} \right)\)
D. Hàm số f(x) đồng biến trên (a;b) khi và chỉ khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyyzImRaaGimaiaacYca % cqGHaiIicaWG4bGaeyicI48aaeWaaeaacaWGHbGaai4oaiaadkgaai % aawIcacaGLPaaaaaa!4407! f'\left( x \right) \ge 0,\forall x \in \left( {a;b} \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0JaaGimaaaa!3B31! f'\left( x \right) = 0\) tại hữu hạn giá trị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabgI % GiopaabmaabaGaamyyaiaacUdacaWGIbaacaGLOaGaayzkaaaaaa!3C8A! x \in \left( {a;b} \right)\)
-
Câu 5:
Cho hàm số y=f(x) có đồ thị như hình vẽ sau:
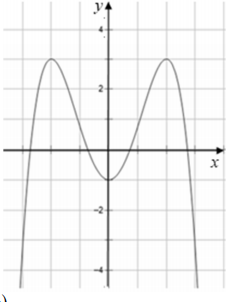
Số nghiệm của phương trình \(\frac{1-f(x)}{1+f(x)}=2\) là?
A. 3
B. 1
C. 2
D. 4
-
Câu 6:
Cho hàm số y=f(x) có đồ thị như hình vẽ.
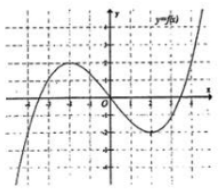
Tìm số nghiệm thuộc \(\left[-\frac{\pi}{6} ; \frac{5 \pi}{6}\right]\) của phương trình \(f(2 \sin x+2)=1 ?\)
A. 2
B. 3
C. 1
D. 0
-
Câu 7:
Cho hàm số \(f(x)=x^{4}-4 x^{2}+3\) có đồ thị là đường cong trong hình bên. Hỏi phương trình \(\left(x^{4}-4 x^{2}+3\right)^{4}-4\left(x^{4}-4 x^{2}+3\right)^{2}+3=0\) có bao nhiêu nghiệm thực phân biệt ?
8A. 8
B. 4
C. 10
D. 9
-
Câu 8:
Cho đồ thị hàm số y=f(x) có đồ thị như hình vẽ. Tìm số nghiệm của phương trình f(x)=x
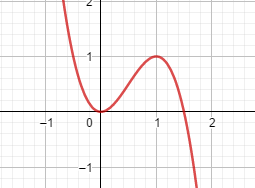
A. 0
B. 1
C. 2
D. 3
-
Câu 9:
Cho hàm số y=f(x) có đồ thị như đường cong hình dưới. Phương trình f(x )=1 có bao nhiêu nghiệm ?
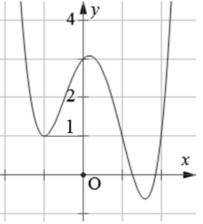
A. 2
B. 4
C. 1
D. 3
-
Câu 10:
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f(x)+1=0\) là
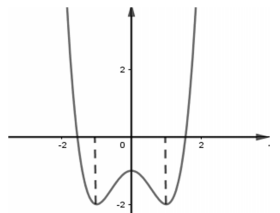
A. 1
B. 3
C. 4
D. 2
-
Câu 11:
Cho hàm số y=f(x) có bảng biến thiên như sau
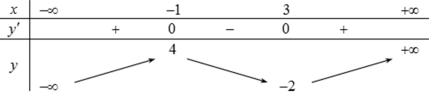
Số nghiệm của phương trình \(f^{2}(x)-4=0\) là?3
A. 3
B. 5
C. 1
D. 2
-
Câu 12:
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
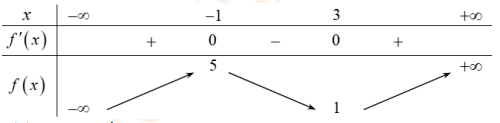
Phương trình f(x)-2=0 có tất cả bao nhiêu nghiệm?
A. 1
B. 3
C. 2
D. 0
-
Câu 13:
:Cho hàm số y=f(x) có bảng biến thiên như sau
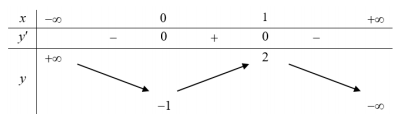
Số nghiệm của phương trình \(f(2-x)-1=0\) là
A. 2
B. 3
C. 0
D. 1
-
Câu 14:
Cho hàm số y=f(x) có bảng biến thiên sau
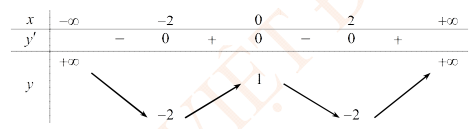
Số nghiệm của phương trình \(2 f(x)+3=0\) là?
A. 4
B. 3
C. 2
D. 1
-
Câu 15:
Cho hàm số \(y=f(x)=x^3+3x^2–x–3\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(y=||x|^3+3x^2–|x|–3|\) có dạng nào trong các đáp án sau đây?
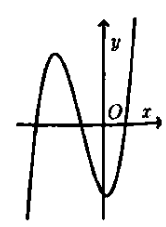
A.
B.
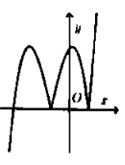
C.
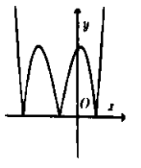
D.
-
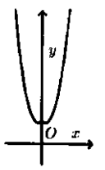
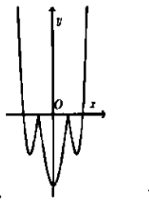
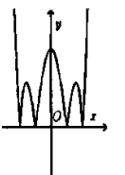
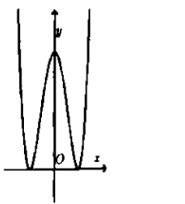
Câu 16:
Cho hàm số \(y=f(x)=x^4–5x^2+4\) có đồ thị như hình vẽ bên.Hỏi đồ thị hàm số \(y=|x^4–5x^2+4| \)có dạng nào trong các đáp án sau đây?
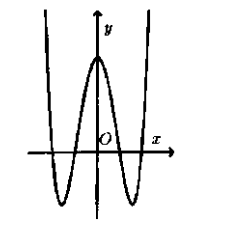
A.
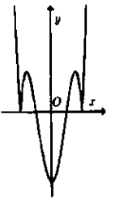
B.
C.
D.
-
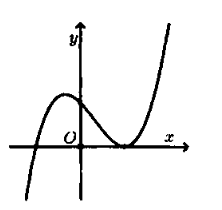
Câu 17:
Cho hàm số \(y=f(x)=x^3–x^2–x+1\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(y=|x^3–x^2–x+1|\) có dạng nào trong các đáp án sau đây?
A.
B.
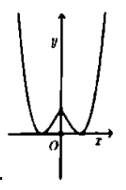
C.
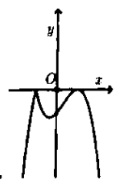
D.
-
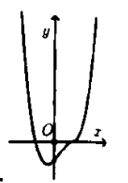
Câu 18:
Hàm số \(y=(x-2)(x^2-1)\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số \(y=|(x-2).|x-1|.(x+1)|\)
.png)
A.
.png)
B.
.png)
C.
.png)
D.
.png)
-
Câu 19:
Hàm số có đồ thị \(y=(x-2)(x^2-1)\)như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số \(y=(|x|)-2)(x^2-1)\)?
.png)
A.
.png)
B.
.png)
C.
.png)
D.
.png)
-
Câu 20:
Cho hàm số \(y=\frac{2x-1}{x-1}\)có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số \(y=\frac{|2x-1|}{x-1}\)
.png)
A.
.png)
B.
.png)
C.
.png)
D.
.png)
-
Câu 21:
Cho hàm số \(y=\frac{2x-1}{x-1}\)có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số \(y=|\frac{2x-1}{x-1}|\)?
.png)
A.
.png)
B.
.png)
C.
.png)
D.
.png)
-
Câu 22:
Cho hàm số \(y=\frac{2x-1}{x-1}\)có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số \(y=\frac{2x-1}{|x-1|}\)?
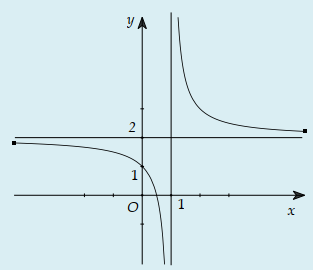
A.
B.
C.
D.
-
Câu 23:
Hàm số \(y=(x-2)(x^2-1)\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số \(y=(x-2)|x-1|(x+1)\)
.png)
A.
.png)
B.
.png)
C.
.png)
D.
.png)
-
Câu 24:
Hàm số \(y=(x-2)(x^2-1)\)có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số \(y=|x-2|(x^2-1)\)?
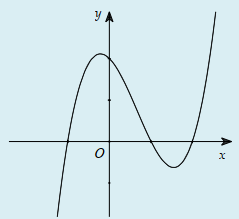
A.
B.
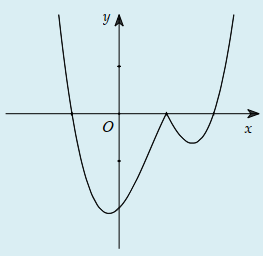
C.
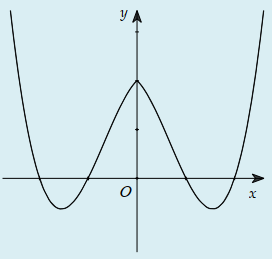
D.
-
Câu 25:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\)và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=|f(x)|?
.png)
A.
.png)
B.
.png)
C.
.png)
D.
.png)
-
Câu 26:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\)và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(|x|)?
.png)
A.
.png)
B.
.png)
C.
.png)
D.
.png)
-
Câu 27:
Cho hàm số xác định, liên tục \(\mathbb{R}\) trên và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=-f(x)?
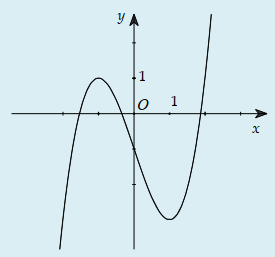
A.
B.
C.
D.
-
Câu 28:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\)và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(-x)?
A.
B.
C.
.png)
D.
-
Câu 29:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\backslash{\{1\}}\) và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(x+1)?
A.
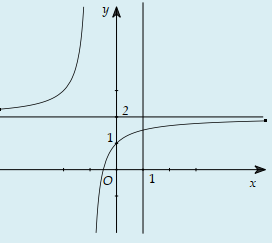
B.
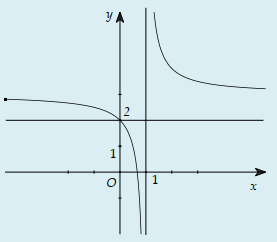
C.
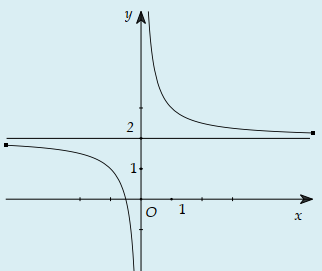
D.
-
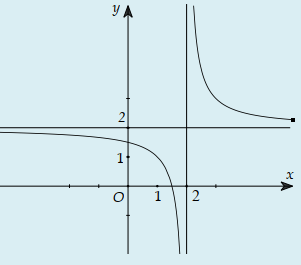
Câu 30:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(x)-1
.png)
A.
.png)
B.
.png)
C.
.png)
D.
.png)
-
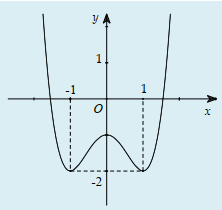
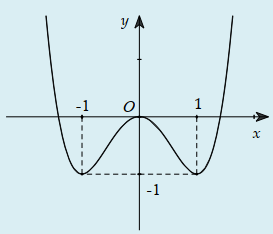
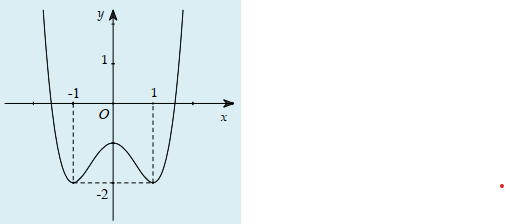
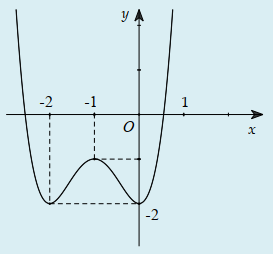
Câu 31:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(x)+1?
A.
B.
C.
D.
-
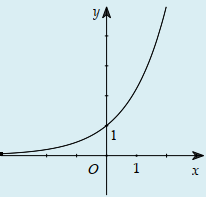
Câu 32:
Cho hàm số y=f(x) xác định, liên tục trên và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số \(y=f(x)+1\)
A.
B.
C.
D.
-
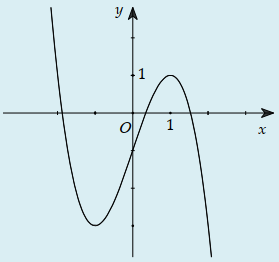
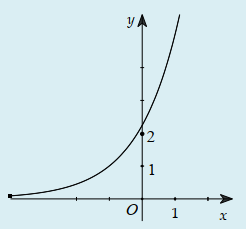
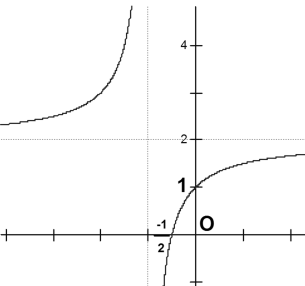
Câu 33:
Đồ thị sau đây là của hàm số nào?
A. \(y=\frac{2x+1}{x+1}\)
B. \(y=\frac{x-1}{x+1}\)
C. \(y=\frac{x+2}{x+1}\)
D. \(y=\frac{x+3}{1-x}\)
-
Câu 34:
Đồ thị trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?.png)
A. \(y=\frac{x+1}{x-1}\)
B. \(y=\frac{2x+1}{x-1}\)
C. \(y=\frac{x+2}{x-1}\)
D. \(y=\frac{x+2}{1-x}\)
-
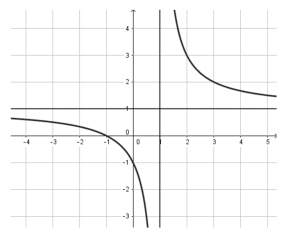
Câu 35:
Đồ thị sau đây là của hàm số nào:
A. \(y=\frac{x+1}{x-1}\)
B. \(y=\frac{x-1}{x+1}\)
C. \(y=\frac{2x+1}{2x-2}\)
D. \(y=\frac{-x}{1-x}\)
-
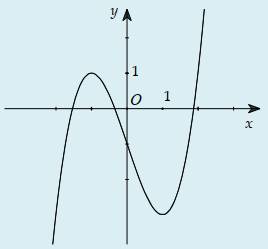
Câu 36:
Đường cong hình bên dưới là đồ thị hàm số nào trong 4 hàm số sau:
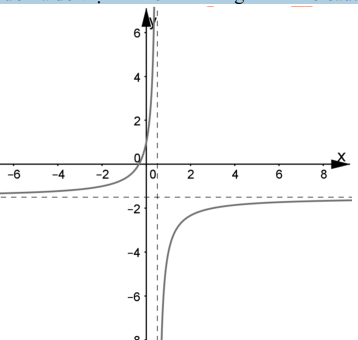
A. \(y=\frac{3x-1}{1-x}\)
B. \(y=\frac{3x+1}{1-2x}\)
C. \(y=\frac{3x-1}{-1-2x}\)
D. \(y=\frac{3x-2}{1-x}\)
-
Câu 37:
Hình vẽ bên là đồ thị của hàm số sau đây?
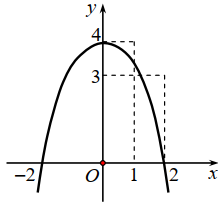
A. \(y=4-\frac{x^4}{4}\)
B. \( y = 4 - x² \)
C. \(y=4-\frac{x^2}{2}-\frac{x^4}{8}\)
D. \(y=4-\frac{x^2}{4}-\frac{x^4}{16}\)
-
Câu 38:
Đường cong hình bên là đồ thị của một hàm số nào trong bốn hàm số dưới đây
.png)
A. \(y = x⁴ - 4x³ + 4x² \)
B. \(y = x² - 4x + 4\)
C. \(y = -x⁴ + 4x³ - 4x² \)
D. \( y = -x² + 4x - 4\)
-
Câu 39:
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
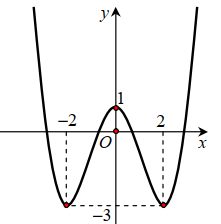
A. \(y = -x ^4 + 8x^ 2 + 1 \)
B. \(y = x^4 - 8x^2 + 1 \)
C. \(y = -x^3 + 3x^2 + 1 \)
D. \(y = | x| ³ - 3x^ 2 + 1\)
-
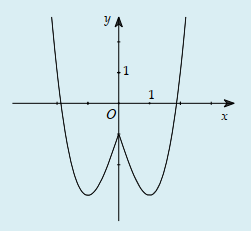
Câu 40:
Hình ảnh bên là đồ thị của hàm số nào sau đây?
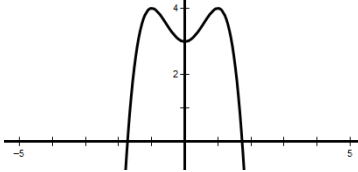
A. \(y = x⁴ - 2x² -3\)
B. \(y = x⁴ + 2x² -3 \)
C. \(y = -x⁴ + 2x² +3 \)
D. \(y = - x⁴ - 2x² + 3 \)
-
Câu 41:
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?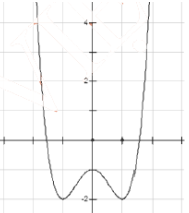
A. \(y = x⁴ - 2x² -1.\)
B. \(y = -x⁴ + 2x² -1\)
C. \(y = x⁴ + 2x² -1\)
D. \(y = \frac{x^4}{4} + 2x² -1 \)
-
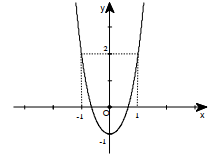
Câu 42:
Đường cong hình bên là đồ thị của hàm số nào trong các hàm số sau?
A. \(y = x² -1\)
B. \(y = x⁴ + 2x² -1\)
C. \(y = -x⁴ - 2x² -1\)
D. \(y = x³ + 2x² -1\)
-
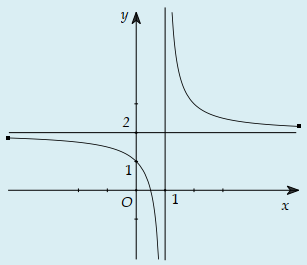
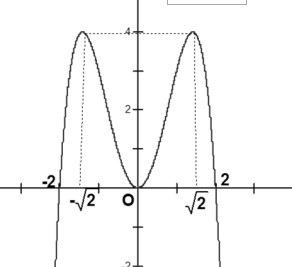
Câu 43:
Đồ thị sau đây là của hàm số nào ?
A. \(y = -x⁴ + 4x ² . \)
B. \(y = -x ⁴ - 2x ² .\)
C. \(y = x ⁴ - 3x ² .\)
D. \(y = -\frac{1}{4}x ⁴ + 3x ²\)
-
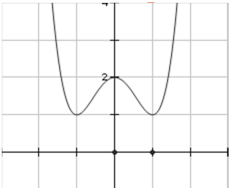
Câu 44:
Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A,B,C,D dưới đây. Hỏi hàm số đó là hàm số nào?
A. \(y = x⁴ - 2x² -1.\)
B. \(y = x⁴ - 2x² +1.\)
C. \(y = x⁴ - 2x²\)
D. \(y = x⁴ - 2x² +2\)
-
Câu 45:
Đường cong trong hình vẽ sau đây là đồ thị của hàm số nào?
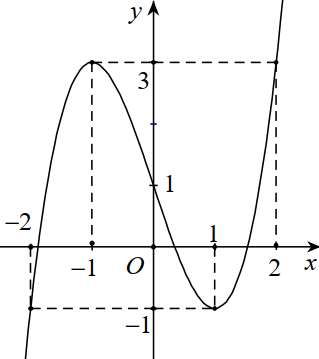
A. \( y = -x³ + 3x +1.\)
B. \(y = x⁴ - 2x² +1.\)
C. \( y = x³ -3x +1.\)
D. \(y = x^3 - 3x² +1.\)
-
Câu 46:
Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên?
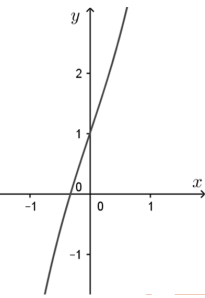
A. \(y = x³ + 3x +1\)
B. \(y = x³ -3x +1\)
C. \(y = -x³ -3x +1\)
D. \(y = -x³ + 3x +1\)
-
Câu 47:
Đồ thị dưới đây là của hàm số nà0?
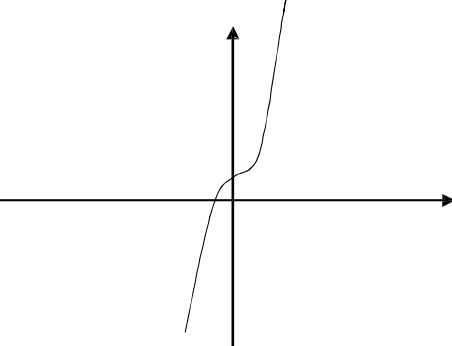
A. \( y = x³ - 3x² +1 \)
B. \( y = x³ +x² +1 \)
C. \( y = -x³+3x² +1 \)
D. \( y = x³ + 3x +1 \)
-
Câu 48:
Đồ thị sau đây là đồ thị của hàm số nào?
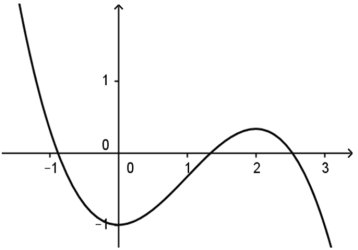
A. \(y = -x⁴ - x² -1\)
B. \(y = x⁴ - 2x² -1 \)
C. \(. y = - \frac{1}{3} x³ + x² -1\)
D. \(. y = \frac{1}{3} x³ -2x² +2\)
-
Câu 49:
Đường cong sau đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
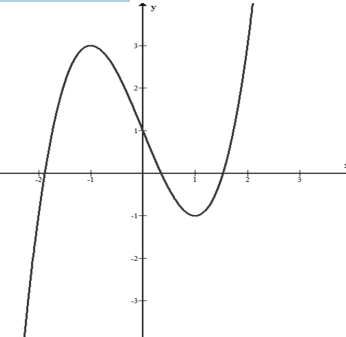
A. \(y=f(x)=x^3-3x+1\)
B. \(y=f(x)=x^3-3x-1\)
C. \(y=f(x)=-x^3+3x+1\)
D. \(y=f(x)=-x^3+3x-1\)
-
Câu 50:
Đồ thị hình bên là của hàm số nào?. Chọn một khẳng định ĐÚNG.
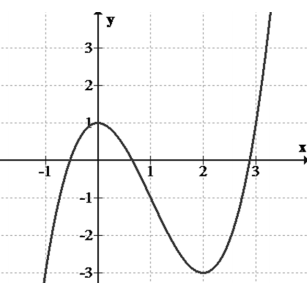
A. \(y=x^3-3x^2+1\)
B. \(y=-\frac{x^3}{3}+x^2+1\)
C. \(y=2x^3-6x^2+1\)
D. \(y=-x^3-3x^2+1\)
