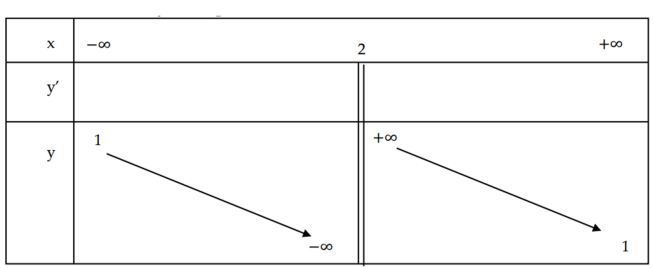
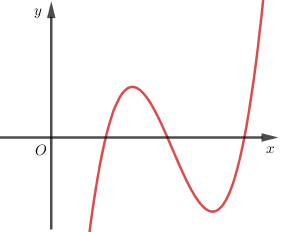
Cho hàm số y=f(x) có bảng biến thiên như hĩnh vẽ.
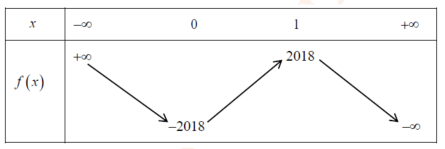
Hỏi phương trình \(|f(x+2017)-2018|=2019\) có bao nhiêu nghiệm?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét đồ thị hàm số \(y=f(x+2017)-2018\) có được bằng cách tịnh tiến đồ thị hàm số y=f(x) song song với trục Ox sang trái 2017 đơn vị, rồi sau đó tịnh tiến song song với trục Oy xuống dưới 2018 đơn vị.
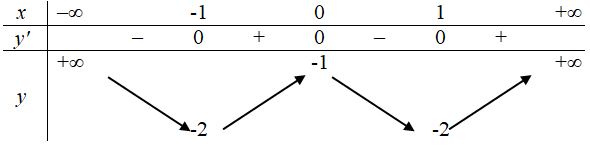
Ta được bảng biến thiên của hàm số \(y=f(x+2017)-2018\) như sau

Khi đó đồ thị hàm số \(|f(x+2017)-2018|\) gồm hai phần:
+ Phần đồ thị của hàm số \(y=g(x)=f(x+2017)-2018\) nằm phía trên trục hoành.
+ Phần đối xứng của đồ thị \(y=g(x)=f(x+2017)-2018\) nằm phía dưới trục hoành.
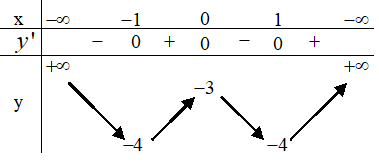
Do đó ta có được bảng biến thiên của hàm số \(y=|g(x)|\) như sau

Dựa vào bảng thiên ta thấy đồ thị hàm số \(y=|g(x)|=|f(x+2017)-2018|\) và đồ thị hàm số y=2019 cắt nhau tại 4 điểm phân biệt.
Suy ra phương trình \(|f(x+2017)-2018|=2019\) có 4 nghiệm phân biệt.



.png)
 8
8.png)
.png)