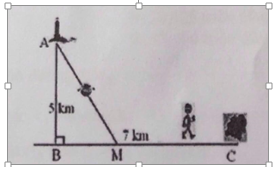
Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển AB=5km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng 7km. Người canh hải đăng có thể chèo đò từ A đến M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C với vận tốc 6km/h. Vị trí của điểm M cách B một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi độ dài đoạn MB là x,(0≤x≤7,km) ⇒ MC=7−x
Tam giác ABM vuông tại B ⇒
\( \Rightarrow AM = \sqrt {B{M^2} + A{B^2}} = \sqrt {{x^2} + {5^2}} = \sqrt {{x^2} + 25} \)
Thời gian người đó đi từ A tới C:
\( \frac{{\sqrt {{x^2} + 25} }}{4} + \frac{{7 - x}}{6}\)
Xét hàm số
\(\begin{array}{l} y' = \frac{x}{{4\sqrt {{x^2} + 25} }} - \frac{1}{6}\\ y' = 0 \Leftrightarrow \frac{x}{{4\sqrt {{x^2} + 25} }} - \frac{1}{6} = 0 \Leftrightarrow \frac{x}{{4\sqrt {{x^2} + 25} }} = \frac{1}{6} \Leftrightarrow 3x = 2\sqrt {{x^2} + 25} \Leftrightarrow 9{x^2} = 4{x^2} + 100 \Leftrightarrow {x^2} = 20 \Rightarrow x = 2\sqrt 5 \end{array}\)
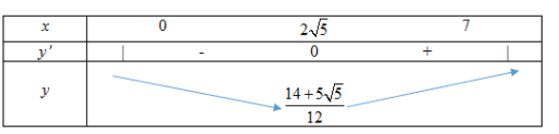
Bảng biến thiên:
Vậy, để người đó đến C nhanh nhất thì khoảng cách từ B đến M là \(2\sqrt5\)
Chọn: A
Câu hỏi liên quan
-
Hàm số \(y = {x^4} - 2{x^2} + 4\) có bao nhiêu điểm cực trị?
-
Số điểm cực đại của hàm số \(f\left( x \right) = - 4{{\rm{x}}^4} - 2{{\rm{x}}^2} + 4\) là
-
Đồ thị hàm số \(y = {x^4} - 3{x^2} + 5\) có bao nhiêu điểm cực tiểu?
-
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số y = x3+ x2+ mx - 1 nằm bên phải trục tung. Tìm số phần tử nguyên của tập hợp (−5;6)∩S.
-
Điểm cực tiểu của đồ thị hàm số \(y = \frac{1}{4}{x^4} + 2{x^2} - 2\) là:
-
Cho hàm số \(y = \frac{{{x^2} - 4x + 8}}{{x - 2}}\). Số điểm cực trị của hàm số là
-
Cho hàm y =f(x) số có \(f^{\prime}(x)<0, \forall x \in \mathbb{R}\) . Tìm tất cả các giá trị thực của x để \(f\left(\frac{1}{x}\right)>f(2)\)
-
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên.
Khẳng định nào sau đây là sai?
-
Cho hàm số y=f(x) có \(f'\left( x \right) = \left( {3x + 5} \right){\left( {x - 1} \right)^2}\left( {{x^2} - 3} \right)\). Điểm cực tiểu của hàm số là
-
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị A(0;0), B(1;1) thì các hệ số a, b, c, d có giá trị lần lượt là:
-
Điểm cực đại của đồ thị hàm số \(y = - {x^4} + {x^2} + 3\) là:
-
Tìm m để hàm số y = x4 – 2mx2 + 2m + m4 – 5 đạt cực tiểu tại x = -1
-
Hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
-
Trong các hàm số dưới đây, hàm số nào có đúng 2 cực trị?
-
Đồ thị của hàm số \(y = – {x^3} + 3{x^2} + 9x + 1\) có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB ?
-
Số điểm cực đại của hàm số \(f\left( x \right) = {{\rm{x}}^4} + \frac{5}{4}{{\rm{x}}^2} - 12\) là
-
Cho \(x \in\left(0 ; \frac{\pi}{2}\right)\). Chọn mệnh đề đúng trong các mệnh đề sau:
-
Hàm số y = (m – 3)x3 – 2mx2 + 3 không có cực trị khi
-
Tìm tất cả các giá trị của tham số m để hàm số \(y = - \frac{x^3}{3} + mx² - 2mx +1 \) có cực đại tại x=1
-
Số điểm cực đại của hàm số \(f\left( x \right) = \frac{1}{5}{{\rm{x}}^4} - \frac{4}{3}{{\rm{x}}^2} + 2\) là
