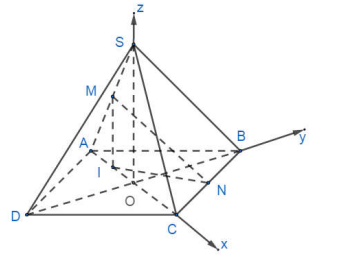
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O . Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC . Biết \(M N=\frac{a \sqrt{6}}{2}\) , tính sin của góc giữa đường thẳng MN và mặt phẳng (SBD).

A. \(\frac{\sqrt{2}}{5}\)

B. \(\frac{\sqrt{3}}{3}\)

C. \(\frac{\sqrt{5}}{5}\)

D. \(\sqrt{3}\)

Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Môn: Toán Lớp 12

Chủ đề: Phương pháp toạ độ trong không gian

Bài: Phương trình đường thẳng trong không gian

Lời giải:

Báo sai

Gọi I hình chiếu của M lên (ABCD) , suy ra I là trung điểm của AO .

Khi đó \(C I=\frac{3}{4} A C=\frac{3 a \sqrt{2}}{4}\) .

Áp dụng định lý cosin ta có:

\(\begin{aligned} &N I=\sqrt{C N^{2}+C I^{2}-2 C N \cdot C I \cdot \cos 45^{\circ}}=\sqrt{\frac{a^{2}}{4}+\frac{9 a^{2}}{8}-2 \cdot \frac{a}{2} \cdot \frac{3 a \sqrt{2}}{4} \cdot \frac{\sqrt{2}}{2}}=\frac{a \sqrt{10}}{4}\\ &\text { Do } \Delta M I N \text { vuông tại } I \text { nên } M I=\sqrt{M N^{2}-N I^{2}}=\sqrt{\frac{3 a^{2}}{2}-\frac{5 a^{2}}{8}}=\frac{a \sqrt{14}}{4} \text { . }\\ &\text { Mà } M I / / S O, M I=\frac{1}{2} S O \Rightarrow S O=\frac{a \sqrt{14}}{2} \text { . } \end{aligned}\)

Chọn hệ trục tọa độ Oxyz như hình vẽ.

Khi đó ta có tọa độ các điểm:\(O(0 ; 0 ; 0), \quad B\left(0 ; \frac{\sqrt{2}}{2} ; 0\right), \quad D\left(0 ;-\frac{\sqrt{2}}{2} ; 0\right), \quad C\left(\frac{\sqrt{2}}{2} ; 0 ; 0\right)\)

\(N\left(\frac{\sqrt{2}}{4} ; \frac{\sqrt{2}}{4} ; 0\right), A\left(-\frac{\sqrt{2}}{2} ; 0 ; 0\right), S\left(0 ; 0 ; \frac{\sqrt{14}}{2}\right), M\left(-\frac{\sqrt{2}}{4} ; 0 ; \frac{\sqrt{14}}{4}\right)\)

\(\begin{aligned} &\text { Khi đó } \overrightarrow{M N}=\left(\frac{\sqrt{2}}{2} ; \frac{\sqrt{2}}{4} ;-\frac{\sqrt{14}}{4}\right), \overrightarrow{S B}=\left(0 ; \frac{\sqrt{2}}{2} ;-\frac{\sqrt{14}}{2}\right), \overrightarrow{S D}=\left(0 ;-\frac{\sqrt{2}}{2} ;-\frac{\sqrt{14}}{2}\right) \text { . }\\ &\text { Véctơ pháp tuyến mặt phẳng }(S B D): \vec{n}=[\overrightarrow{S B}, \overrightarrow{S D}]=(-\sqrt{7} ; 0 ; 0)\\ &\text { Suy ra } \sin (M N,(S B D))=\frac{|\overrightarrow{M N} \cdot \vec{n}|}{|\overline{M N}| \cdot|\vec{n}|}=\frac{\left|\frac{\sqrt{2}}{2} \cdot(-\sqrt{7})\right|}{\frac{\sqrt{6}}{2} \cdot \sqrt{7}}=\frac{\sqrt{3}}{3} \end{aligned}\)