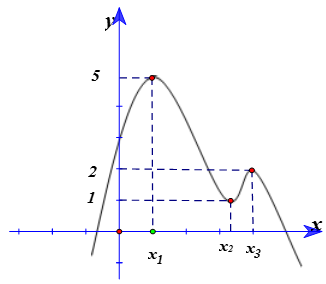
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị của hàm đạo hàm \(f’\left( x \right)\) như hình vẽ và \(f\left( b \right) = 1\). Số giá trị nguyên của \(m \in \left[ { – 5;5} \right]\) để hàm số \(g\left( x \right) = \left| {{f^2}\left( x \right) + 4f\left( x \right) + m} \right|\) có đúng 5 điểm cực trị là
.jpg.png)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
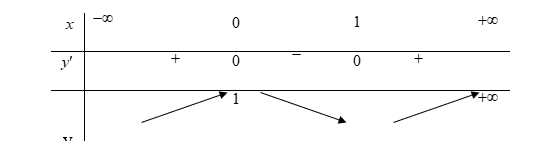
Báo saiTa có bảng biến thiên của \(f\left( x \right)\)
.png)
Xét hàm số \(h\left( x \right) = {f^2}\left( x \right) + 4f\left( x \right) + m\)
\(\begin{array}{l}\Rightarrow h’\left( x \right) = 2f’\left( x \right)f\left( x \right) + 4f’\left( x \right)\\ \Rightarrow h’\left( x \right) = 2f’\left( x \right)\left[ {f\left( x \right) + 2} \right]\end{array}\)
\(\begin{array}{l}h’\left( x \right) = 0 \Rightarrow 2f’\left( x \right)\left[ {f\left( x \right) + 2} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}f’\left( x \right) = 0\\f\left( x \right) = – 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = a;x = b\\x = c\left( {c < a} \right)\end{array} \right.\end{array}\)
Pt có 3 nghiệm phân biệt \( \Rightarrow \) có 3 điểm cực trị
Xét \(h\left( x \right) = 0\)
\( \Leftrightarrow {f^2}\left( x \right) + 4f\left( x \right) = – m\left( 2 \right)\)
Để \(g\left( x \right) = \left| {h\left( x \right)} \right|\) có 5 điểm cực trị khi và chỉ khi PT \(\left( 2 \right)\) có 2 nghiệm đơn hoặc nghiệm bội lẻ phân biệt
Xét hàm số \(t\left( x \right) = {f^2}\left( x \right) + 4f\left( x \right)\)
Ta có Bảng biến thiên của \(t\left( x \right)\):
.png)
Từ YCBT \( \Leftrightarrow t\left( x \right) = – m\) có hai nghiệm đơn hoặc nghiệm bội lẻ pb
\( \Leftrightarrow m \in \left\{ { – 5; – 4; – 3; – 2; – 1;0;1;2;3} \right\}.\)