525 câu trắc nghiệm môn Toán rời rạc
tracnghiem.net chia sẻ 525 câu trắc nghiệm môn Toán rời rạc (có đáp án) dành cho các bạn sinh viên chuyên ngành có thêm tư liệu học tập, ôn tập chuẩn bị cho kì thi kết thúc học phần sắp diễn ra. Nội dung gồm những vấn đề cơ bản nhất của toán học rời rạc lý thuyết tổ hợp, lý thuyết đồ thị, lý thuyết độ phức tạp, đại số Boole.,…Để việc ôn tập trở nên hiệu quả hơn, các bạn có thể ôn theo từng phần trong bộ câu hỏi này bằng cách trả lời lần lượt các câu hỏi cũng như so sánh đáp và lời giải chi tiết được đưa ra. Sau đó các bạn hãy chọn tạo ra đề ngẫu nhiên để kiểm tra lại kiến thức mình đã ôn tập được nhé!
Chọn hình thức trắc nghiệm (30 câu/60 phút)
-
Câu 1:
Đồ thị liên thông G có một đỉnh có bậc bằng một thì:
A. G có chu trình Hamilton
B. G có chu trình Euler
C. G không có chu trình Hamilton
D. G không có chu trình
-
Câu 2:
Người ta xếp ngẫu nhiên 5 lá phiếu có ghi số thứ tự từ 1 đến 5 cạnh nhau. Có bao nhiêu cách xếp để các phiếu phân thành 2 nhóm chẵn lẻ riêng biệt.
A. 2
B. 20
C. 10
D. 24
-
Câu 3:
Có bao nhiêu trường hợp về chân trị của bộ biến mệnh đề (q1,q2,..,qn)?
A. 2n
B. 2n
C. 2n+1
D. 2n-1
-
Câu 4:
Một tổ hợp chập k của n phần tử:
A. Là một cách xếp có thứ tự n phần tử đó
B. Là một bộ không kể thứ tự gồm k thành phần khác nhau lấy từ n phần tử đã cho.
C. Là bộ có thứ tự gồm k thành phần lấy từ n phần tử của tập đã cho.
D. Là bộ có thứ tự gồm k thành phần lấy ra từ n phần tử đã cho. Các phần tử không được lặp lại.
-
Câu 5:
Trong biểu diễn đồ thị bởi danh sách kề, mỗi đỉnh của đồ thị có một danh sách:
A. Các cạnh kề với đỉnh đó
B. Các bậc của đỉnh kề với đỉnh đó
C. Các đỉnh kề với đỉnh đó
D. Các cạnh kề với cạnh đó
-
Câu 6:
Xác định chân trị của biểu thức ( P → Q ) Λ ( Q → R ) và (P → R) khi P = Q = 1, R=0?
A. 1 và 1
B. 0 và 0
C. 1 và 0
D. 0 và 1
-
Câu 7:
Cho 2 tập A={1, 2, 3}, B={a, b, c, 2}. Trong số các tập dưới đây, tập nào là một quan hệ 2 ngôi từ A tới B?
A. {(1,a), (1,1), (2,a)}
B. {(2, 2), (2,3), (3,b)}
C. {(1,2), (2,2), (3,a)}
D. {(2,c), (2,2), (b,3)}
-
Câu 8:
Cho quan hệ R = {(1,1), (1,2), (2,2), (2,3), (3,1), (3,3)} trên tập {1,2,3}. Hỏi phát biểu nào sau đây là đúng?
A. R là quan hệ tương đương
B. R là quan hệ thứ tự
C. R có tính bắc cầu
D. R không có tính bắc cầu
-
Câu 9:
Sự khác nhau giữa thuật toán Prim và thuật toán Kruskal:
A. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, liên thuộc trong khi thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc.
B. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, liên thuộc với một đỉnh thuộc cây khung và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây khung và không tạo thành chu trình.
C. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, liên thuộc với các đỉnh đã thuộc cây và không tạo thành chu trình.
D. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, không liên thuộc với một đỉnh thuộc cây khung và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây khung và không tạo thành chu trình.
-
Câu 10:
Thuật toán được qọi là đệ quy nếu:
A. Giải quyết bài toán bằng cách chia nhỏ bài toán ban đầu tới các bài toán cơ sở
B. Giải quyết bài toán bằng cách chia đôi bài toán ban đầu thành các bài toán con
C. Giải quyết bài toán bằng cách rút gọn liên tiếp bài toán ban đầu tới bài toán cũng như vậy nhưng có dữ liệu đầu vào nhỏ hơn.
D. Giải quyết bài toán bằng cách rút gọn liên tiếp bài toán ban đầu tới bài toán cũng như vậy nhưng có dữ liệu đầu vào bằng một nửa.
-
Câu 11:
Giá trị của luồng cực đại trong mạng:
A. Lớn hơn khả năng thông qua của mọi lát cắt.
B. Bằng khả năng thông qua của một lát cắt.
C. Không vượt quá khả năng thông qua của lát cắt hẹp nhất trong mạng.
D. Không vượt quá khả năng thông qua của lát cắt lớn nhất trong mạng.
-
Câu 12:
Công thức nào sau đây đúng. Cho n và k là các số nguyên dương với n ≥ k. Khi đó:
A.
B.
C.
D.
-
Câu 13:
Cho 2 tập A, B với là:
A. 20
B. 15
C. 35
D. 5
-
Câu 14:
Câu nào sau đây KHÔNG là một mệnh đề?
A. Hôm nay không phải thứ hai.
B. x là bạn cùng lớp với Lan.
C. Nếu hôm nay trời nắng thì tôi sẽ đi chơi.
D. Có một người trong lớp không biết môn toán Rời rạc.
-
Câu 15:
Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A với:
R= {(1,1), (2,2), (3,3),(4,4), (5,5), (6,6), (1,3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}
Đồ thị biểu diễn quan hệ R là
A.
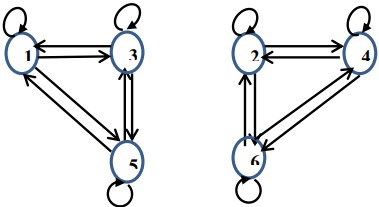
B.

C.
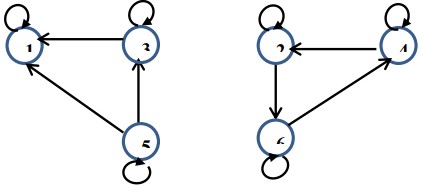
-
Câu 16:
Để chứng minh một quy tắc suy luận đúng ta thường sử dụng các phương pháp:
A. Định nghĩa, biến đổi tương đương logic
B. Lập bảng giá trị chân lý và kết luận theo định nghĩa
C. Biến đổi tương đương logic
D. Chứng minh trực tiếp
-
Câu 17:
Đồ thị vô hướng G = (V,E) được gọi là liên thông nếu.
A. Giữa hai đỉnh bất kỳ luôn tồn tại đường đi từ u đến v.
B. Nếu , thì tồn tại v khác u sao cho v liên thông với u.
C. Nếu , thì với mọi v khác u đều kề với u.
D. Nếu , thì tồn tại đỉnh v khác u kề với u.
-
Câu 18:
Trong bất kỳ một nhóm có 367 người, thế nào cũng có:
A. Nhiều nhất một người có cùng ngày sinh.
B. Ít nhất một người có cùng ngày sinh.
C. Ít nhất hai người có cùng ngày sinh.
D. Nhiều nhất một người có cùng ngày sinh.
-
Câu 19:
Cho n, r là các số nguyên không âm sao cho . Khi đó:
A. C(n, r)=C(n+r-1, r)
B. C(n, r)=C(n, r-1)
C. C(n, r)=C(n, n-r)
D. C(n, r)=C(n-r, r)
-
Câu 20:
Tìm hệ số của x9 trong khai triển của (2 - x)20
A. C(20,10).210
B. (20,9).211
C. – C(20,9)211
D. – C(20,10)29
-
Câu 21:
Trong các luật sau, luật nào là luật luỹ đẳng?
A.
B.
C.
D.
-
Câu 22:
Một chỉnh hợp lặp chập k của n phần tử:
A. Là bộ có thứ tự gồm k thành phần lấy ra từ n phần tử đã cho. Các phần tử không được lặp lại.
B. Là bộ có thứ tự gồm k thành phần lấy từ n phần tử của tập đã cho.
C. Là một bộ không kể thứ tự gồm k thành phần khác nhau lấy từ n phần tử đã cho.
D. Là một cách xếp có thứ tự n phần tử đó.
-
Câu 23:
Cho đồ thị như hình vẽ. Hãy cho biết kết quả thực hiện thuật toán DFS(1):
.jpg)
A. 1, 2, 7, 4, 5, 10, 3, 6, 9, 8
B. 1, 2, 3, 6, 9, 4, 5, 10, 8, 7
C. 1, 2, 3, 4, 5, 10, 6, 9, 7, 8
D. 1, 2, 7, 8, 3, 6, 9, 5, 10, 4
-
Câu 24:
Công thức nào sau đây đúng. Cho n là số nguyên dương, khi đó là:
A. 2n-1
B. 2n
C. 2n+1
D. 2n -1
-
Câu 25:
Phương trình x1 + x2 + x3 = 11 có bao nhiêu nghiệm nguyên không âm?
A. 78
B. 165
C. 990
D. 21
-
Câu 26:
Có bao nhiêu số nguyên dương gồm đúng 3 chữ số chia hết cho 3 hoặc chia hết cho 4?
A. 75
B. 300
C. 224
D. 449
-
Câu 27:
Có bao nhiêu xâu nhị phân độ dài bằng 6 và chứa 4 số 0 liên tiếp.
A. 4
B. 8
C. 10
D. 12
-
Câu 28:
Có bao nhiêu cách xếp các chữ a, b, c, d, e sao cho chữ b không đi liền sau chữ a và d không đi liền sau chữ c?
A. 120
B. 78
C. 72
D. 96
-
Câu 29:
Nếu G = (V,E) là một đơn đồ thị vô hướng thì: (Chọn phương án đúng)
A. Ma trận kề gồm các phần tử đối xứng nhau qua đường chéo chính
B. Ma trận kề gồm các phần tử không đối xứng nhau qua đường chéo chính
C. Các phần tử trên đướng chéo chính bằng 1
D. Các phần tử trên đường chéo phụ bằng 1
-
Câu 30:
Quy tắc (luật )suy luận nào là cơ sở của suy diễn sau: Trường chất lượng cao thì có cán bộ giảng dạy giỏi. Trường có cán bộ giảng dạy giỏi thì có sinh viên giỏi. Vậy trường chất lượng cao thì có sinh viên giỏi.
A. Luật khẳng định
B. Luật phủ định
C. Luật tam đoạn luận
D. Luật tam đoạn luận rời

















