Đề thi HK1 môn Toán 11 năm 2022-2023
Trường THPT Trần Đại Nghĩa
-
Câu 1:
Điều kiện xác định của hàm số \(y=\sqrt{\frac{1-\sin x}{{{\sin }^{2}}x}}\) là:
A. \(x\ne \frac{\pi }{2}+k\pi \)
B. \(x\ne k2\pi \)
C. \(x\ne \frac{\pi }{2}+k2\pi \)
D. \(x\ne k\pi \)
-
Câu 2:
M, m lần lượt là GTLN, GTNN của hàm số \(y=4\sin \left( x-\dfrac{5\pi }{4} \right)-3\cos \left( x-\dfrac{5\pi }{4} \right)\) . Khi đó:
A. \(M=5,m=-5\)
B. \(M=1,m=-1\)
C. \(M=7,m=1\)
D. \(M=1,m=7\)
-
Câu 3:
Phương trình \(\sin x=\cos x\) có nghiệm là:
A. \(x=\frac{\pi }{4}+k2\pi \)
B. \(x=-\frac{\pi }{4}+k2\pi \)
C. \(\left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \frac{{5\pi }}{4} + k2\pi \end{array} \right.\)
D. Một kết quả khác
-
Câu 4:
Phương trình \(2{{\sin }^{2}}x-1=0\) có nghiệm là:
A. \(x=\frac{\pi }{4}+k2\pi \)
B. \(x=\frac{\pi }{4}+k\pi \)
C. \(x=\frac{\pi }{4}+k\frac{\pi }{2}\)
D. \(x=\frac{\pi }{4}+k\frac{\pi }{4}\)
-
Câu 5:
Phương trình \(2{{\sin }^{2}}x+\sin x-3=0\) có nghiệm là:
A. \(k\pi \)
B. \(\frac{\pi }{2}+k\pi \)
C. \(\frac{\pi }{2}+k2\pi \)
D. \(-\frac{\pi }{6}+k2\pi \)
-
Câu 6:
Phương trình \(\sin x\cos x\cos 2x=0\) có nghiệm là:
A. \(k\pi \)
B. \(\frac{k\pi }{2}\)
C. \(\frac{k\pi }{4}\)
D. \(\frac{k\pi }{8}\)
-
Câu 7:
Phương trình \(\sin x+\sqrt{3}\cos x=2\) có nghiệm là:
A. \(\frac{\pi }{6}+k2\pi \)
B. \(-\frac{\pi }{6}+k\pi \)
C. \(\frac{5\pi }{6}+k2\pi \)
D. \(x=\frac{5\pi }{6}+k\pi \)
-
Câu 8:
Phương trình \(\tan x=\cot x\) có nghiệm là:
A. \(\frac{\pi }{2}+\left( k+1 \right)\frac{\pi }{2}\)
B. \(\frac{\pi }{2}+k\pi \)
C. \(\frac{\pi }{4}+k\frac{\pi }{2}\)
D. \(x = \frac{\pi }{2} + \frac{{k\pi }}{2}\)
-
Câu 9:
Phương trình \(2{{\cos }^{2}}x+5\sin x=4\) có nghiệm âm lớn nhất bằng:
A. \(-\frac{7\pi }{6}\)
B. \(-\frac{5\pi }{6}\)
C. \(-\frac{11\pi }{6}\)
D. \(-\frac{\pi }{6}\)
-
Câu 10:
Một họa sĩ có 8 bức tranh khác nhau. Hỏi có bao nhiêu cách xếp các bức tranh này theo một thứ tự nhất định ?
A. 40320
B. 20160
C. 360
D. 10620
-
Câu 11:
Một lớp có 10 học sinh được chọn, bầu vào 3 chức vụ khác nhau: lớp trưởng, lớp phó, bí thư (không kiêm nhiệm). Số cách lựa chọn khác nhau là:
A. 30
B. 1000
C. 720
D. 120
-
Câu 12:
Một người có 4 cái quần, 6 cái áo, 3 cái cà vạt. Để chọn 1 quần, 1 áo, 1 cà vạt thì số cách chọn khác nhau là:
A. 13
B. 72
C. 34
D. 24
-
Câu 13:
Với đa giác lồi 10 cạnh, số đường chéo là:
A. 90
B. 40
C. 35
D. 55
-
Câu 14:
Nghiệm của phương trình \({{x}^{2}}C_{x-1}^{x-4}=A_{4}^{2}C_{x+1}^{3}-xC_{x-1}^{3}\)là:
A. 4
B. 5
C. 6
D. 7
-
Câu 15:
Trong biểu thức khai triển \({{\left( 1-x \right)}^{6}}\), hệ số của số hạng chứa \({{x}^{3}}\) là:
A. -10
B. -20
C. 10
D. 20
-
Câu 16:
Hệ số của \({{x}^{10}}{{y}^{19}}\) trong khai triển \({{\left( x-2y \right)}^{29}}\) là:
A. \({{2}^{19}}C_{29}^{10}\)
B. \(-{{2}^{19}}C_{29}^{10}\)
C. \(C_{29}^{10}\)
D. \(-C_{29}^{10}\)
-
Câu 17:
Tổng các hệ số trong khai triển \({{\left( \frac{1}{x}+{{x}^{4}} \right)}^{n}}\) là 1024. Tìm hệ số chứa \({{x}^{5}}\).
A. 120
B. 210
C. 792
D. 972
-
Câu 18:
Tìm số hạng không chứa x trong khai triển \({{\left( x-\frac{1}{x} \right)}^{n}}\) biết \(C_{n}^{2}C_{n}^{n-2}+2C_{n}^{2}C_{n}^{3}+C_{n}^{3}C_{n}^{n-3}=100\)
A. 9
B. 8
C. 6
D. Đáp số khác
-
Câu 19:
Gieo ngẫu nhiên 2 con súc sắc cân đối và đồng chất. Tìm xác suất của các biến cố sau. A “Tổng số chấm xuất hiện là 7”, C “Tích số chấm xuất hiện là 12”.
A. \(\frac{1}{6};\frac{1}{9}\)
B. \(\frac{30}{36};\frac{1}{6}\)
C. \(\frac{5}{18};\frac{1}{3}\)
D. \(\frac{1}{9};\frac{1}{9}\)
-
Câu 20:
Một hộp chứa 5 viên bi đỏ và 6 viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp đó. Tính xác suất để viên bi lấy ra cò màu đỏ.
A. \(\frac{5}{11}\)
B. \(\frac{1}{3}\)
C. \(\frac{2}{3}\)
D. \(\frac{3}{4}\)
-
Câu 21:
Một lớp có 20 học sinh, trong đó có 2 cán bộ lớp. Chọn ra 3 học sinh. Tính xác suất để có ít nhất 1 cán bộ lớp?
A. \(\frac{5}{6}\)
B. \(25\)
C. \(\frac{2}{7}\)
D. \(\frac{27}{95}\)
-
Câu 22:
Biết \(M'\left( -3;2 \right)\) là ảnh của \(M\left( 1;-2 \right)\) qua \({{T}_{\overrightarrow{u}}},M''\left( 2;3 \right)\) là ảnh của M’ qua \({{T}_{\overrightarrow{v}}}\). Tọa độ \(\overrightarrow{u}+\overrightarrow{v}=?\)
A. \(\left( 1;5 \right)\)
B. \(\left( 1;-5 \right)\)
C. \(\left( -1;-5 \right)\)
D. \(\left( -1;5 \right)\)
-
Câu 23:
Phép \({{V}_{\left( O;-3 \right)}}\) biến đường tròn \(\left( C \right):{{x}^{2}}+{{y}^{2}}-2x+4y-4=0\) thành đường tròn có phương trình:
A. \({{\left( x+3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}=9\)
B. \({{\left( x-3 \right)}^{2}}+{{\left( y+6 \right)}^{2}}=81\)
C. \({{\left( x-3 \right)}^{2}}+{{\left( y+6 \right)}^{2}}=9\)
D. \({{\left( x+3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}=81\)
-
Câu 24:
Cho hình chóp S.ABCD. Chọn khẳng định sai?
A. A, B, C, D đồng phẳng.
B. S, B, C, D không đồng phẳng.
C. S không nằm trong mặt phẳng (ABCD).
D. S, A, B, C đồng phẳng.
-
Câu 25:
Trong các mệnh đề sau mệnh đề nào đúng ?
A. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
B. Hai đường thẳng không có điểm chung thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng phân biệt không song song thì chéo nhau.
-
Câu 26:
Cho tứ diện ABCD. Trong các mệnh đề sau mệnh đề nào SAI?
A. AB và CD chéo nhau.
B. A, B, C, D không đồng phẳng.
C. AD và BC không cắt nhau.
D. AC cắt BD.
-
Câu 27:
Cho 2 đường thẳng a, b chéo nhau. Trên a lấy hai điểm A, B. Trên b lấy 2 điểm C, D. Mệnh đề nào sau đây sai?
A. AB và CD chéo nhau
B. AC và BD chéo nhau
C. AD và BC chéo nhau
D. AC, BD cùng thuộc 1 mặt phẳng
-
Câu 28:
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi với AB và CD không song song. Gọi I là giao điểm của 2 đường thẳng AB và CD. Gọi d là giao tuyến các mặt (SAB) và (SCD). Tìm d ?
A. \(d\equiv SO\)
B. \(d\equiv AC\)
C. \(d\equiv BD\)
D. \(d\equiv SI\)
-
Câu 29:
Cho hình chóp S.ABC có ABC là tam giác. Gọi M, N lần lượt là hai điểm thuộc cạnh AC, BC sao cho MN không song song với AB. Gọi đường thẳng a là giao tuyến của (SMN) và (SAB). Tìm a?
A. \(a\equiv SQ\) với Q là giao điểm của BH với MN, H là điểm thuộc SA.
B. \(a\equiv MI\) với I là giao điểm của hai đường thẳng MN và AB.
C. \(a\equiv SO\) với O là giao điểm của hai đường thẳng AM và BN
D. \(a\equiv SI\) với I là giao điểm của hai đường thẳng MN và AB.
-
Câu 30:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và BC. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với:
A. BJ
B. AD
C. BI
D. IJ
-
Câu 31:
Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mặt phẳng (P). Gọi M là điểm nằm giữa S và A; N là điểm nằm giữa S và B; giao điểm của hai đường thẳng AC và BD là O; giao điểm của hai đường thẳng CM và SO là I; giao điểm của hai đường thẳng NI và SD là J. Tìm giao điểm của mp(CMN) với đường thẳng SO là:
A. A
B. J
C. I
D. B
-
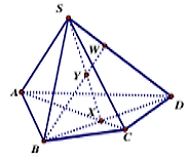
Câu 32:
Cho hình chóp S.ABCD như hình vẽ bên dưới. CÓ ABCD là tứ giác lồi. Với W là điểm thuộc cạnh SD, X là giao điểm của hai đường thẳng AC với BD và Y là giao điểm 2 đường thẳng SX với BW. Gọi P là giao điểm của DY và (SAB). Khẳng định nào dưới đây đúng?
A. P là giao điểm của 2 đường thẳng DY và SB
B. P là giao điểm của 2 đường thẳng DY và SA
C. P là giao điểm của 2 đường thẳng DY và AB
D. P là giao điểm của 2 đường thẳng DW và SC
-
Câu 33:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, G là trọng tâm tam giác BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là:
A. Điểm C
B. Giao điểm của đường thẳng MG và đường thẳng AN
C. Điểm N
D. Giao điểm của đường thẳng MG và đường thẳng BC
-
Câu 34:
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Giao tuyến của (SAD) và (SBC) là:
A. SO
B. Sx // AD // BC
C. SA
D. SD
-
Câu 35:
Cho hình chóp S.ABCD có đáy là đa giác lồi, O là giao điểm của AC và BD, B’, C’ lần lượt là trung điểm của SB, SC. SD cắt (AB’C’) tại D’. Khi đó:
A. Các đường thẳng AC’, B’D’, SO đồng quy.
B. B’, C’, D’ thẳng hàng.
C. Các đường thẳng AC’, B’D’, SO đồng phẳng.
D. S, O, D’ thẳng hàng.
-
Câu 36:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và AC, d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC) là:
A. d cắt (ABC)
B. \(d\subset \left( ABC \right)\)
C. d không song song (ABC)
D. d // (ABC)
-
Câu 37:
Cho hình chóp S.ABCD có đáy hình bình hành. Gọi M, N, Q lần lươt là trung điểm của BC, CD, SA. Thiết diện của (MNQ) với hình chóp là:
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
-
Câu 38:
Cho tứ diện có tất cả các cạnh bằng nhau và bằng a, M là trung điểm của AB. Mp(P) qua M song song với BC và CD cắt tứ diện theo 1 thiết diện có diện tích là:
A. \(\frac{{{a}^{2}}\sqrt{3}}{16}\)
B. \(\frac{{{a}^{2}}\sqrt{3}}{8}\)
C. \(\frac{{{a}^{2}}\sqrt{3}}{12}\)
D. \(\frac{{{a}^{2}}\sqrt{3}}{4}\)
-
Câu 39:
Cho tứ diện ABCD, M thuộc đoạn AB, thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) đi qua M song song với BD và AC là:
A. Hình bình hành
B. Hình thoi
C. Tam giác
D. Hình thang cân
-
Câu 40:
Cho tứ diện ABCD có tất cả các cạnh đều bằng a. Gọi \({{G}_{1}},{{G}_{2}}\) lần lượt là trọng tâm tam giác BCD và ACD. Khi đó đoạn thẳng \({{G}_{1}}{{G}_{2}}\) bằng:
A. \(\frac{a}{4}\)
B. \(\frac{a}{3}\)
C. \(\frac{2a}{3}\)
D. \(\frac{3a}{2}\)
