Tìm m để hàm số \(y=\frac{(m+1) x-1}{2 m x+1}\) đồng biến trên khoảng (0;1).
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ TH1: Với m =0 hàm số trở thành y=x-1 là hàm số đồng biến trên \(\mathbb{R}\) nên đồng biến trên khoảng (0;1).
+TH2: Với \(m\ne0\) ta có;
\(y'=\frac{3m+1}{(2mx+1)^2}\)
Hàm số dồng biến trên khoảng (0;1) khi và chỉ khi
\(\left\{\begin{array}{c} -\frac{1}{2 m} \notin(0 ; 1) \\ m+1+2 m>0 \end{array} \Leftrightarrow\left\{\begin{array}{c} -\frac{1}{2 m} \notin(0 ; 1) \\ m>-\frac{1}{3} \end{array}\right.\right.\)
Xét hàm số \(g(m)=-\frac{1}{2 m} \text { trên khoảng }\left(-\frac{1}{3} ;+\infty\right)\). ta có:
\(g^{\prime}(m)=\frac{1}{2 m^{2}}>0, \forall m \neq 0\)
bảng biến thiên hàm số g(m) trên \(\left(-\frac{1}{3} ;+\infty\right)\)
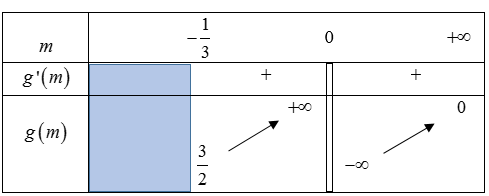
\(g(m) \notin(0 ; 1), \forall m \in\left(-\frac{1}{3} ;+\infty\right) \backslash\{0\}\)
Từ hai trường hợp suy ra \(m<-\frac{1}{3}\)
Câu hỏi liên quan
-
Tìm tham số m để hàm số \(y=\frac{\sin x+4}{\sin x+m}\) nghịch biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right)\)?
-
Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
\(y = \frac{{2x + 1}}{{x + 1}}\) (I) ; y = - x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
-
Hỏi hàm số \(y\; = \;\frac{{{x^2}\; - \;3x\; + \;5}}{{x\; + \;1}}\) nghịch biến trên các khoảng nào ?
-
Số giá trị nguyên của tham số m để hàm số \(y=\left(4-m^{2}\right) x^{3}+(m-2) x^{2}+x+m-1(1)\) đồng biến trên \(\mathbb{R}\) là
-
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số \(y=\frac{m-1}{3} x^{3}+m x^{2}+(3 m-2) x\) đồng biến trên \((-\infty ;+\infty)\)?
-
Cho đồ thị hàm số y = −x3 như hình vẽ. Hàm số y = −x3 nghịch biến trên khoảng:
-
Tập hợp các giá trị thực của m để hàm số \(y=\frac{-3 x^{2}+m x-2}{2 x-1}\) luôn nghịch biến trên từng khoảng xác định là
-
Hàm số \(y = - 2{x^3} + 3{x^2} - 3\) đồng biến trên các khoảng:
-
Tìm khoảng đồng biến của hàm số \(f\left( x \right) = x + {\cos ^2}x\)
-
Hàm số \(y=-x^{4}+8 x^{2}+6\) đồng biến trên khoảng nào dưới đây? -
Tìm các giá trị thực của m để hàm số \(y=\frac{1}{3} x^{3}-2 x^{2}+m x-1\) đồng biến trên R.
-
Cho hàm số y = - x3 + 3x2 – 3x + 7. Mệnh đề nào sau đây là đúng?
-
Cho hàm số \(y = f(x) = 2{x^3} + 6{x^2} + 6x - 2017\). Mệnh đề nào dưới đây sai
-
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây.
Hỏi có bao nhiêu giá trị nguyên của tham số m để phương trình \(f(3 \cos x+1)=-\frac{m}{2}\) có nghiệm trên đoạn -
Tìm tất cả các giá trị thực của tham số m đề hàm số nghịch biến trên khoảng (1;+∞)
-
Với giá trị nào của m hàm số \(y=\frac{m x+4}{x+m}\) nghịch biến trên từng khoảng xác định của nó:
-
Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 ngàn đồng một ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 ngàn đồng thì có thêm 2 phòng trống. Giám đốc phải chọn giá phòng mới là bao nhiêu để thu nhập của khách sạn trong ngày là lớn nhất.
-
Cho phương trình x3- 3x2+ 1- m = 0 (1) . Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa mãn x1 < 1< x2 < x3 khi
-
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpdaWc % aaqaaiabgkHiTiaaikdaaeaacqGHsislcaWG4bGaey4kaSIaaGymaa % aaaaa!41AF! y = f\left( x \right) = \frac{{ - 2}}{{ - x + 1}}\) có tính chất
-
Cho hàm số y = f(x) có đạo hàm trên R thoả f( 2) = f( -2) = 0 và đồ thị của hàm số y = f’ (x) có dạng như hình bên. Hàm số y = (f( x)) 2 nghịch biến trên khoảng nào trong các khoảng sau ?
