ADMICRO
Cho x,y∈R thỏa mãn x+y≠−1 và x2+y2+xy=x+y+1. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=xyx+y+1. Tính M+m.
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
ZUNIA12
Lời giải:
Báo saiVới điều kiện x+y≠−1;x2+y2+xy=x+y+1 ta có P=xyx2+y2+xy .
Nếu y=0 thì {x≠−1x2−x−1=0⇔x=1±√52 . Khi đó P=0 .
Nếu y≠0 thì P=xy(xy)2+xy+1 . Đặt t=xy . Ta có P=tt2+t+1,t∈R .
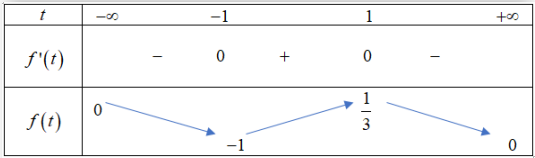
Xét f(t)=tt2+t+1,t∈R⋅f′(t)=−t2+1(t2+t+1)2;f′(t)=0⇔t=±1
Từ bẳng biến thiên:
M=13 tại {xy=1x2+y2+xy=x+y+1⇔{x=y3x2−2x−1=0
⇔{x=y[x=1x=−13⇔[x=y=1x=y=−13
m=−1 tại {xy=−1x2+y2+xy=x+y+1⇔{x=−yx2−1=0⇔{x=−y[x=1x=−1
⇔[{x=1y=−1{x=−1y=1
Vậy M+m=−23 .
ZUNIA9
AANETWORK



.png)
.PNG)