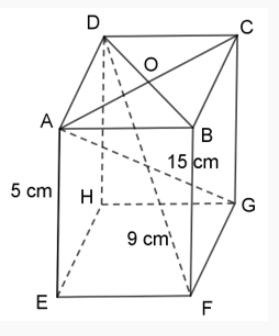
Cho hình lăng trụ đứng ABCD.EFGH có đáy là hình thoi. Biết đường cao AE = 5 cm, đường chéo AG = 15 cm, DF = 9 cm. Tính cạnh AB của đáy?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Gọi O là giao của 2 đường chéo DB và AC trong mặt đáy (ABCD)
của hình lăng trụ đứng ABCD.EFGH.
Ta có: DCG⊥AC, BF⊥BD (Vì ABCD.EFGH là hình lăng trụ đứng)
Ta lại có:
AE = CG = BF = 5 cm (Vì AE, CG, BF là các cạnh bên của hình lăng trụ đứng ABCD.EFGH)
Áp dụng định lý Pitago trong tam giác vuông ACG, ta có:
\(\begin{array}{*{20}{c}} {}&{A{C^2} + C{G^2} = A{G^2}}\\ {}&{ \Leftrightarrow A{C^2} + {5^2} = {{15}^2}}\\ {}&{ \Leftrightarrow A{C^2} = {{15}^2} - {5^2} = 200}\\ {}&{ \Rightarrow AC = 10\sqrt 2 {\rm{\;}}cm} \end{array}\)
Áp dụng định lý Pitago trong tam giác vuông DBF, ta có:
\(\begin{array}{*{20}{c}} {}&{D{B^2} + B{F^2} = D{F^2}}\\ {}&{ \Leftrightarrow D{B^2} + {5^2} = {9^2}}\\ {}&{ \Leftrightarrow D{B^2} = {9^2} - {5^2} = 56}\\ {}&{ \Rightarrow DB = 2\sqrt {14} {\rm{\;}}cm} \end{array}\)
Ta có:
\(\begin{array}{l} B{\rm{D}} \bot AC\\ AO = OC = \frac{1}{2}AC = \frac{{10\sqrt 2 }}{2} = 5\sqrt 2 {\rm{\;}}cm,{\rm{\;}}OB = O{\rm{D}} = \frac{1}{2}DB = \frac{{2\sqrt {14} }}{2} = \sqrt {14} {\rm{\;}}cm \end{array}\)
(Vì ABCD là hình thoi)
Áp dụng định lý Pitago trong tam giác vuông AOB, ta có:
\(\begin{array}{*{20}{c}} {}&{O{A^2} + O{B^2} = A{B^2}}\\ {}&{ \Leftrightarrow {{(5\sqrt 2 )}^2} + {{(\sqrt {14} )}^2} = A{B^2}}\\ {}&{ \Leftrightarrow 64 = A{B^2}}\\ {}&{ \Rightarrow AB = 8{\rm{\;}}cm} \end{array}\)
Vậy AB = 8 cm.
Câu hỏi liên quan
-
Cho hình lăng trụ đứng đáy là hình thoi có hai đường chéo lần lượt là 8cm và 10cm. Tính chiều cao của lăng trụ đứng biết thể tích của lăng trụ đứng là 360 cm3.
-
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều, M là trung điểm cạnh BC, AA’ = AM = a. Diện tích xung quanh và thể tích của hình lăng trụ lần lượt là:
-
Một lăng trụ đứng có đáy là hình chữ nhật có các kích thức 3 cm, 8 cm. Chiều cao của hình lăng trụ đứng là 2 cm. Tính thể tích của hình lăng trụ đứng.
-
Tính thể tích của khối lăng trụ sau:
.png)
-
Thể tích hình lăng trụ đứng theo các kích thước ở hình là
.PNG)
-
Lăng trụ đứng có kích thước như ở hình thì thể tích của nó là
.PNG)
-
Tính thể tích của hình dưới đây:
.png)
-
Diện tích toàn phần và thể tích của hình lăng trụ đứng có kích thước như hình vẽ lần lượt là:
.png)
-
Thể tích của lăng trụ đứng có chiều cao h và đáy là hình thang cân, đáy lớn là 2a, các cạnh còn lại bằng a
bằng: -
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình thang vuông ABCD vuông tại A, B (AD∥BC) và BC = 12 cm, AD = 16 cm, CD = 5 cm, đường cao AA′=6 cm. Thể tích của hình lăng trụ là:
-
Tính thể tích của hình dưới đây:
.png)
-
Gàu xúc của một xe xúc đất được mô tả như một lăng trụ đứng đáy tam giác với kích thước đã cho trên hình. Em hãy tính xem để hết đống cát 40 m3, xe phải xúc ít nhất bao nhiêu gàu ?
.jpg)
-
Diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và đáy hình vuông cạnh a lần lượt là:
-
Thể tích của một lăng trụ đứng theo các kích thước như hình là:
.PNG)
-
Hình khối sau đây có phải là hình lăng trụ đứng không? Tính thể tích của khối.
.jpg)
-
Thể tích của một bể nước hình lăng trụ đứng có các kích thước cho ở hình vẽ là:
.png)
-
Tính thể tích hình:
.PNG)
-
Tìm diện tích toàn phần của hình lăng trụ đứng (theo kích thước đã cho trên hình).
-
Cho hình lăng trụ đứng (ABCD.A'B'C'D' ) có đáy là hình thang vuông ABCD vuông tại A, B (AD//BC) và BC = 12 cm, AD = 16 cm, CD = 5 cm, đường cao AA' = 6 ;cm. Thể tích của hình lăng trụ là:
-
Tính thể tích hình hình dưới đây:
.png)
