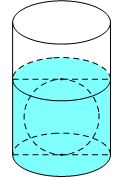
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(1\), mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích \(V\) của khối cầu ngoại tiếp hình chóp đã cho.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi \(O\) là tâm đường tròn tam giác \(ABC\) suy ra \(O\) là trọng tâm, \(H\) là trung điểm\(AB\), kẻ đường thẳng qua \(O\) song song \(SH\) cắt \(SC\) tại \(N\) ta được \(NO\bot \left( ABC \right)\), gọi \(M\) là trung điểm\(SC\), \(HM\)cắt \(NO\) tại \(I.\)
Ta có \(HS=HC\) nên \(HM\bot SC\Rightarrow IS=IC=IA=IB=r\)
Ta có
\(\angle NIM=\angle HCS={{45}^{0}},\frac{CN}{CS}=\frac{CO}{CH}=\frac{2}{3}\Rightarrow CN=\frac{2}{3}\frac{\sqrt{6}}{2}=\frac{\sqrt{6}}{3}\Rightarrow SM=\frac{\sqrt{6}}{4},SN=\frac{1}{\sqrt{6}}\)
Suy ra \(NM=SM-SN=\frac{\sqrt{6}}{12}\)
\(\Delta NMI\) vuông tại \(M\)\(\tan {{45}^{0}}=\frac{NM}{IM}\Rightarrow IM=NM=\frac{\sqrt{6}}{12}\)
Suy ra \(r=IC=\sqrt{I{{M}^{2}}+M{{C}^{2}}}=\sqrt{\frac{5}{12}}\)
Vậy \(V=\frac{4}{3}\pi {{r}^{3}}=\frac{5\sqrt{15}\pi }{54}\).
