Cho hai số thực x y , thay đổi thỏa mãn điều kiện \(x^{2}+y^{2}=2\) . Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức \(P=2\left(x^{3}+y^{3}\right)-3 x y\) . Giá trị của M + n bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
\(P=2\left(x^{3}+y^{3}\right)-3 x y=2(x+y)\left(x^{2}-x y+y^{2}\right)-3 x y=2(x+y)\left[(x+y)^{2}-3 x y\right]-3 x y\)
\(\text { Tù } x^{2}+y^{2}=2 \Rightarrow(x+y)^{2}-2 x y=2 \Rightarrow x y=\frac{(x+y)^{2}}{2}-1\)
Đặt \(x+y=t \text { và thay vào } P \text { ta được }\)
\(P=2 t\left[t^{2}-3\left(\frac{t^{2}}{2}-1\right)\right]-3\left(\frac{t^{2}}{2}-1\right)=-t^{3}-\frac{3}{2} t^{2}+6 t+3\)
\(\text { Mặt khác } 2=(x+y)^{2}-2 x y \geq(x+y)^{2}-\frac{(x+y)^{2}}{2}=\frac{(x+y)^{2}}{2} \Rightarrow(x+y)^{2}-4 \leq 0\)
\(-2 \leq x+y \leq 2 \Rightarrow t \in[-2 ; 2]\)
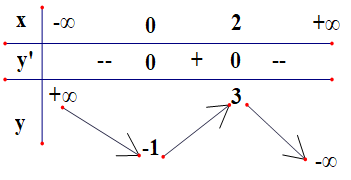
\(\text { Khảo sát hàm số } P=-t^{3}-\frac{3}{2} t^{2}+6 t+3 \text { trên } t \in[-2 ; 2] \text { ta được } m=\min\limits _{[-2 ; 2]} P=-7 ; M=\max \limits_{[-2 ; 2]} P=\frac{13}{2}\)
\(\text { Vậy } M+m=-\frac{1}{2} \text { . }\)
Câu hỏi liên quan
-
Cho hàm số \(f\left( x \right)\) có đạo hàm là \(f’\left( x \right)\). Đồ thị hàm số \(y = f’\left( x \right)\) được cho như hình vẽ bên. Biết rằng \(f\left( 0 \right) + f\left( 2 \right) = f\left( 1 \right) + f\left( 3 \right)\). Giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ {0;3} \right]\) là
.jpg.png)
-
Hàm số \(y=\frac{x^{2}-3 x}{x+1}\) đạt giá trị lớn nhất trên đoạn [0;3] là:
-
Giá trị nhỏ nhất của hàm số \(y = x + \frac{9}{x}\) trên đoạn \(\left[ {2;4} \right]\) là:
-
Cho hàm số y = f(x) có đồ thị y = f'(x) như hình vẽ.
.jpg.png)
Xét hàm số \(g(x) = f(x) – \frac{1}{3}{x^3} – \frac{3}{4}{x^2} + \frac{3}{2}x + 2018.\) Mệnh đề nào dưới đây đúng?
-
Cho hàm số \(f\left( x \right) = \frac{{2\sqrt x + m}}{{\sqrt {x + 1} }}\) với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.
-
Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số \(y=x \sqrt{1-x^{2}}\) . Khi đó M + m bằng
-
GTNN của hàm số \(y\; = \;\frac{x}{{\left( {x + 2} \right)}}\) trên nửa khoảng (-2;4] là
-
Biết hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có M và m lần lượt là GTLN, GTNN của hàm số trên đoạn \(\left[ {0;2} \right]\). Trong các hàm số sau, hàm số nào cũng có GTLN và GTNN tương ứng là M và m?.
-
Giá trị nhỏ nhất của hàm số \(y=x+\frac{9}{x}\)trên đoạn [2;4] là:
-
Một trang chữ của một quyển sách tham khảo Văn học cần diện tích 384 cm2. Biết rằng trang giấy được canh lề trái là 2cm, lề phải là 2 cm, lề trên 3 cm và lề dưới là 3 cm. Trang sách đạt diện tích nhỏ nhất thì có chiều dài và chiều rộng là:
-
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{3x - 11}}{{x + 2}}\text{ trên đoạn } \left[ {1;5} \right]\)
-
Cho hàm số y=f(x) có bảng biến thiên như sau:
.PNG)
\(\begin{equation} \text { Đặt } g(x)=f(\cos x) \text { . } \end{equation}\)Khẳng định nào sau đây đúng?
-
Cho hàm số \(y = \frac{{x + m}}{x}\) thỏa \(\mathop {\min }\limits_{\left[ {1;2} \right]} y + \mathop {\max }\limits_{\left[ {1;2} \right]} y = 8\), với m là tham số thực. Mệnh đề nào dưới đây đúng?
-
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f’\left( x \right)\) như hình bên. Đặt \(g\left( x \right) = 2f\left( x \right) – {\left( {x + 1} \right)^2}\). Mệnh đề nào dưới đây đúng?
.jpg.png)
-
Giá trị nhỏ nhất của hàm số \(f(x)=\frac{x^{2}-x+1}{x-1}\) trên khoảng \((1 ;+\infty)\) là
-
Giá trị nhỏ nhất của hàm số \(y=e^{x}\left(x^{2}-x-1\right)\) trên đoạn [0;2] là
-
Tìm tất cả các giá trị của tham số m để hàm số \(y = {x^3} – 3{x^2} + m\) có giá trị nhỏ nhất trên \(\left[ { – 1;1} \right]\) bằng \(\sqrt 2 \).
-
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f(x) trên [ a; e]?
-
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên dưới. Biết rằng m là tham số thực. Gọi S là tập chứa tất cả các giá trị thực của tham số m để hàm số \(f\left( {3x – m} \right) + 2f\left( {{x^2} – 2x} \right)\) đạt giá trị lớn nhất. Tổng giá trị của tất cả các phần tử thuộc tập S bằng:
.jpg.png)
-
GTLN của hàm số \(y = - {x^2} + 4x + 7\) đạt được khi x bằng:
