ADMICRO
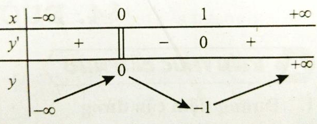
Cho đồ thị hàm số y=f(x)y=f(x) như hình vẽ bên dưới. Biết rằng m là tham số thực. Để hàm số g(x)=2f(2x–m)–f(3x+n)+x2–2xg(x)=2f(2x–m)–f(3x+n)+x2–2x đạt giá trị nhỏ nhất thì giá trị của biểu thức T = 2m + 3n bằng:
.jpg.png)
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
ZUNIA12
Lời giải:
Báo saiNhận thấy –3=f(4)≤f(x)≤f(0)+5⇔{f(x)≥f(4)=–3–f(x)≥–f(0)=–5,∀x∈R.
Xét hàm số g(x)=2f(2x–m)–f(3x+n)+x2–2x=2f(2x–m)–f(3x+n)+(x–1)2–1.
Ta có {f(2x–m)≥f(4)=–3–f(3x+n)≥f(0)=–5(x–1)2≥0⇒g(x)≥2.(–3)–5+0–1=–12.
Dấu bằng xảy ra khi ⇔{2x–m=43x+n=0x+1=0⇔{2–m=43+n=0x=1⇔{m=–2b=–3x=1⇒T=2m+3n=–13.
ZUNIA9
AANETWORK



.jpg.png)











