Cho hai hình cầu đồng tâm \(\left( {O;2} \right)\) và \(\left( {O;\sqrt {10} } \right)\). Một tứ diện ABCD có hai đỉnh A, B nằm trên mặt cầu \(\left( {O;2} \right)\) và các đỉnh C, D nằm trên mặt cầu \(\left( {O;\sqrt {10} } \right)\). Thể tích lớn nhất của khối tứ diện ABCD bằng bao nhiêu?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai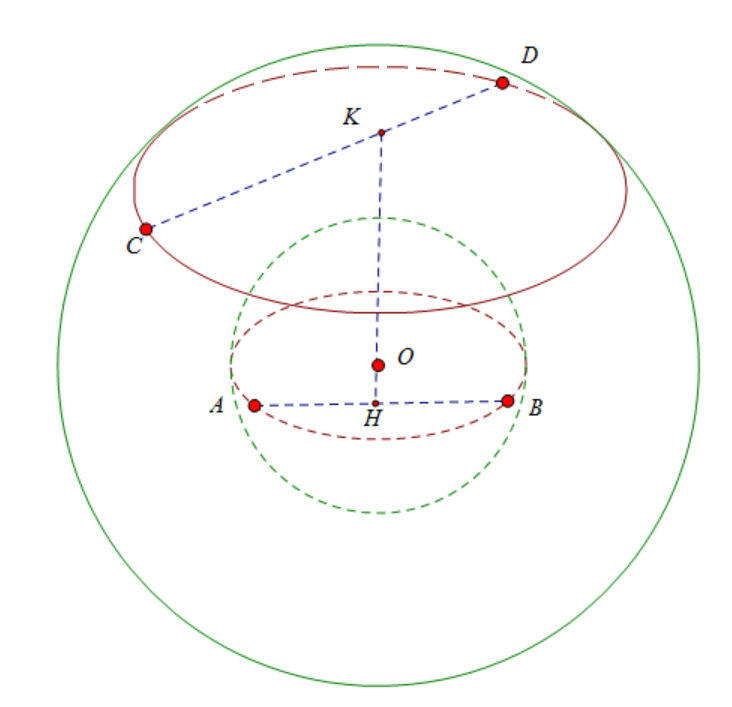
Đặt OK = a, OH = b.
\({V_{ABCD}} = \frac{{AB.CD.HK.\sin \left( {AB;CD} \right)}}{6} \le \frac{{AB.CD.HK}}{6} \le \frac{2}{3}\sqrt {10 – {a^2}} .\sqrt {4 – {b^2}} \left( {a + b} \right)\)
\({V_{ABCD}} \le \frac{2}{3}\frac{{\sqrt 3 }}{{\sqrt 2 }}\sqrt {\left( {10 – {a^2}} \right)\left( {4 – {b^2}} \right)\left( {{a^2} + 2{b^2}} \right)} \)
\({V_{ABCD}} \le \frac{{2\sqrt 3 }}{6}\sqrt {\left( {10 – {a^2}} \right)\left( {8 – 2{b^2}} \right)\left( {{a^2} + 2{b^2}} \right)} \)
\({V_{ABCD}} \le \frac{{2\sqrt 3 }}{6}\sqrt {216} = 6\sqrt 2 \). Dấu xảy ra khi a = 2, b = 1.
Câu hỏi liên quan
-
Cho hình chóp S.ABCD có đáy là hình chữ nhật với \(A C=2 a, \quad B C=a\) . Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng đáy bằng 600 Thể tích của khối chóp đã cho bằng
-
Gọi \(l, h, R\) lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của một hình nón. Đẳng thức nào sau đây đúng?
-
Cho hình chóp có đáy là hình vuông cạnh bằng 4, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(SD,CD,BC.\) Thể tích khối chóp \(S.ABPN\) là \(x,\) thể tích khối tứ diện \(CMNP\) là \(y.\) Giá trị \(x,y\) thỏa mãn bất đẳng thức nào dưới đây:
-
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là a3. Tính thể tích khối chóp S.ABCD
-
Cho lăng trụ tam giác \(ABC.{{A}_{1}}{{B}_{1}}{{C}_{1}}\) có tất cả các cạnh bằng a, góc tại bởi cạnh bên và mặt phẳng đáy bằng \({{30}^{0}}\). Hình chiếu H của điểm A trên mặt phẳng \(\left( {{A}_{1}}{{B}_{1}}{{C}_{1}} \right)\)thuộc đường thẳng \({{B}_{1}}{{C}_{1}}\). Thể tích khối lăng trụ \(ABC.{{A}_{1}}{{B}_{1}}{{C}_{1}}\) bằng:
-
Cho khối chóp \(S.ABC.\) Lấy A', B' lần lượt thuộc SA, SB sao cho \(2SA'=3A'A;\text{ }3SB'=B'B.\) Tỉ số thể tích giữa hai khối chóp \(S.A'B'C\) và \(S.ABC\) là:
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC.
-
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Biết AB = a, AD = 2a, AA’ = 3a. Tính thể tích khối hộp ABCD.A’B’C’D’.
-
Tính thể tích V của khối lập phương \(ABCD.{A_1}{B_1}C{}_1{D_1}\), biết diện tích mặt chéo \(AC{C_1}{A_1}\) bằng \(4\sqrt 2 {a^2}\)
-
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng \(a\), một mặt phẳng (\(\alpha \)) cắt các cạnh AA’; BB’;CC’; DD’ lần lượt tại M, N,P,Q. Biết AM= \(\frac{1}{3}a\), CP = \(\frac{2}{5}a\). Thể tích khối đa diện ABCD.MNPQ là:
-
Cho hình thang vuông ABCD có đường cao AD = 1 , đáy nhỏ AB = 1, đáy lớn CD = 2. Cho hình thang đó quay quanh AB ta được khối tròn xoay có thể tích bằng
-
Cho hình hộp chữ nhật \(ABCD.{A}'{B}'{C}'{D}'\) có đáy là hình vuông, cạnh bên bằng \(4a\) và đường chéo \(5a\) .Tính thể tích hình hộp chữ nhật này.
-
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SB và mặt phẳng đáy bằng 600. Thể tích của khối chóp đã cho bằng
-
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a,\(\widehat{BCD}={{120}^{0}}\) và \(AA'=\frac{7a}{2}\). Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết \(SA \bot (ABCD);\,\,SA = a\sqrt 3 .\) Tính thể tích của khối chóp.
-
Cho khối lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có BB'=a , đáy ABC là tam giác vuông cân tại B và \(A C=a \sqrt{2}\). Thể tích của khối lăng trụ đã cho bằng
-
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy, góc giữa \(SA\) và mặt phẳng \(\left( SBC \right)\) bằng \(45{}^\circ \) ( tham khảo hình bên). Thể tích của khối chóp \(S.ABC\) bằng:
-
Cho khối lăng trụ tam giác\(ABC.A'B'C'\) có thể tích bằng 30 (đơn vị thể tích). Thể tích của khối tứ diện \(AB'C'C\) là:
-
Khối lăng trụ có diện tích đáy bằng \(24\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\), chiều cao bằng 3 \(\left( {{\rm{cm}}} \right)\) thì có thể tích bằng
-
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau tại O và OA = 2, OB = 4, OC = 6. Thể tích khối tứ diện đã cho bằng.
