Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020

THPT Yên Lạc

50 câu

90 phút

9 lượt thi

Câu 1:

Tìm hoành độ các giao điểm của đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaikdacaWG4bGaeyOeI0YaaSaaaeaacaaIXaGaaG4maaqaaiaa % isdaaaaaaa!3CE3! y = 2x - \frac{{13}}{4}\) với đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % igdaaeaacaWG4bGaey4kaSIaaGOmaaaaaaa!3E3A! y = \frac{{{x^2} - 1}}{{x + 2}}\) .

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iaaikdacqGHXcqSdaWcaaqaamaakaaabaGaaGOmaaWcbeaaaOqa % aiaaikdaaaaaaa!3C4D! x = 2 \pm \frac{{\sqrt 2 }}{2}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgkHiTmaalaaabaGaaGymaiaaigdaaeaacaaI0aaaaiaacUda % caWG4bGaeyypa0JaaGOmaaaa!3EA5! x = - \frac{{11}}{4};x = 2\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iaaigdacaGG7aGaamiEaiabg2da9iaaikdacaGG7aGaamiEaiab % g2da9iaaiodaaaa!3FAE! x = 1;x = 2;x = 3\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgkHiTmaalaaabaGaaGymaiaaigdaaeaacaaI0aaaaaaa!3B27! x = - \frac{{11}}{4}\)

Câu 2:

Tìm giá trị nhỏ nhất của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaaGymaiab % gkHiTiaadIhaaaaaaa!3E03! y = \frac{{2x + 1}}{{1 - x}}\) trên đoạn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaaca % aIYaGaai4oaiaaiodaaiaawUfacaGLDbaaaaa!3A1D! \left[ {2;3} \right]\) .

A. 1

B. -2

C. 0

D. -5
Câu 3:

Một tổ học sinh có nam và nữ. Chọn ngẫu nhiên người. Tính xác suất sao cho người được chọn đều là nữ.

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGymaiaaiwdaaaaaaa!3838! \frac{1}{{15}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGymaiaaiwdaaaaaaa!3838! \frac{1}{{15}}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aI4aaabaGaaGymaiaaiwdaaaaaaa!383F! \frac{8}{{15}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGymaiaaiwdaaaaaaa!3838! \frac{8}{{15}}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aI3aaabaGaaGymaiaaiwdaaaaaaa!383E! \frac{7}{{15}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGymaiaaiwdaaaaaaa!3838! \frac{7}{{15}}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGynaaaaaaa!377D! \frac{1}{5}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGymaiaaiwdaaaaaaa!3838! \frac{1}{{5}}\)
Câu 4:

Nghiệm của phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qaciGGJbGaai4BaiaacohacaWG4bGaeyypa0JaeyOeI0IaaGPaVlaa % cckadaWcaaqaaiaaigdaaeaacaaIYaaaaaaa!400C! \cos x = - \,\;\frac{1}{2}\) là :

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgglaXoaalaaabaGaaGOmaiabec8aWbqaaiaaiodaaaGaey4k % aSIaam4AaiaaikdacqaHapaCaaa!4176! x = \pm \frac{{2\pi }}{3} + k2\pi \)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgglaXoaalaaabaGaeqiWdahabaGaaGOnaaaacqGHRaWkcaWG % RbGaeqiWdahaaa!4001! x = \pm \frac{\pi }{6} + k\pi \)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgglaXoaalaaabaGaeqiWdahabaGaaG4maaaacqGHRaWkcaWG % RbGaaGOmaiabec8aWbaa!40BA! x = \pm \frac{\pi }{3} + k2\pi \)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgglaXoaalaaabaGaeqiWdahabaGaaGOnaaaacqGHRaWkcaWG % RbGaaGOmaiabec8aWbaa!40BD! x = \pm \frac{\pi }{6} + k2\pi \)

Câu 5:

Hệ số góc của tiếp tuyến của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiaayk % W7cqGH9aqpcaaMc8+aaSaaaeaacaWG4bWaaWbaaSqabeaacaaI0aaa % aaGcbaGaaGinaaaacaaMc8UaaGPaVlabgUcaRiaaykW7daWcaaqaai % aadIhadaahaaWcbeqaaiaaikdaaaaakeaacaaIYaaaaiaaykW7cqGH % sislcaaIXaGaaGPaVdaa!4ACA! y\, = \,\frac{{{x^4}}}{4}\,\, + \,\frac{{{x^2}}}{2}\, - 1\,\)tại điểm có hoành độ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacaWG4bWdamaaBaaaleaapeGaaGimaaWdaeqaaOGaeyypa0Zdbiab % gkHiTiaaigdaaaa!3AEC! {x_0} = - 1\) bằng :

A. -2

B. Đáp số khác.

C. 2

D. 0
Câu 6:

Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhacqGHRaWkcaaIXaaaaa!3A92! y = x + 1\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaikdaaaaaaa!39DE! y = {x^2}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgkHiTiaaigdaaeaacaWG4bGaey4kaSIa % aGOmaaaaaaa!3D48! y = \frac{{x - 1}}{{x + 2}}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iGacohacaGGPbGaaiOBaiaadIhaaaa!3BCD! y = \sin x\)

Câu 7:

Cho đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGibaacaGLOaGaayzkaaaaaa!384A! \left( H \right)\): \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHsislcaaI0aaabaGaamiEaiab % gkHiTiaaiodaaaaaaa!3E13! y = \frac{{2x - 4}}{{x - 3}}\). Lập phương trình tiếp tuyến của đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGibaacaGLOaGaayzkaaaaaa!384A! \left( H \right)\) tại giao điểm của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGibaacaGLOaGaayzkaaaaaa!384A! \left( H \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4taiaadI % haaaa!37C5! Ox\).

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaikdacaWG4baaaa!39B1! y = 2x\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaaikdacaWG4bGaey4kaSIaaGinaaaa!3C3E! y = - 2x + 4\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaaikdacaWG4bGaeyOeI0IaaGinaaaa!3C49! y = - 2x - 4\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaaikdacaWG4bGaeyOeI0IaaGinaaaa!3C49! y = 2x - 4\)
Câu 8:

Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaaGOmaiaa % dIhacqGHsislcaaIXaaabaGaamiEaiabgUcaRiaaigdaaaaaaa!4076! f\left( x \right) = \frac{{2x - 1}}{{x + 1}}\) xác định trên R \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeSyhHeQaai % ixamaacmaabaGaaGymaaGaay5Eaiaaw2haaaaa!3B2F! \backslash \left\{ 1 \right\}\) . Đạo hàm của hàm số\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaaaa!3965! f\left( x \right)\):

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaI % XaaabaWaaeWaaeaacaWG4bGaey4kaSIaaGymaaGaayjkaiaawMcaam % aaCaaaleqabaGaaGOmaaaaaaaaaa!404E! f'\left( x \right) = \frac{1}{{{{\left( {x + 1} \right)}^2}}}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaI % YaaabaWaaeWaaeaacaWG4bGaey4kaSIaaGymaaGaayjkaiaawMcaam % aaCaaaleqabaGaaGOmaaaaaaaaaa!404F! f'\left( x \right) = \frac{2}{{{{\left( {x + 1} \right)}^2}}}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacqGH % sislcaaIXaaabaWaaeWaaeaacaWG4bGaey4kaSIaaGymaaGaayjkai % aawMcaamaaCaaaleqabaGaaGOmaaaaaaaaaa!413B! f'\left( x \right) = \frac{{ - 1}}{{{{\left( {x + 1} \right)}^2}}}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaI % ZaaabaWaaeWaaeaacaWG4bGaey4kaSIaaGymaaGaayjkaiaawMcaam % aaCaaaleqabaGaaGOmaaaaaaaaaa!4050! f'\left( x \right) = \frac{3}{{{{\left( {x + 1} \right)}^2}}}\)
Câu 9:

Đồ thị sau đây là của hàm số nào?

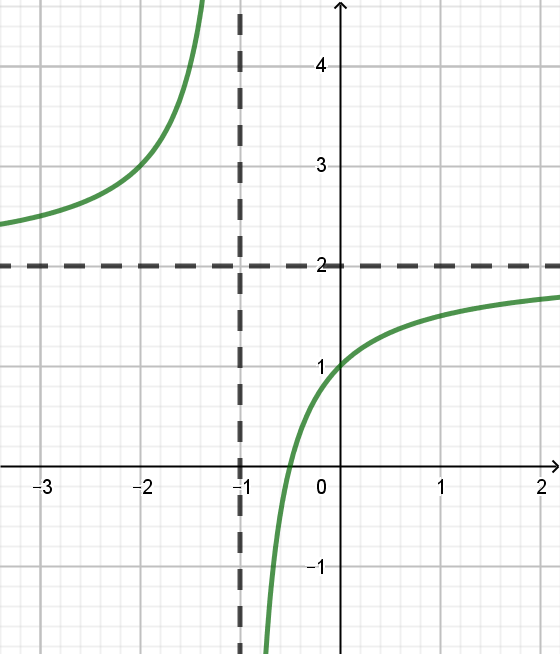
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiab % gUcaRiaaigdaaaaaaa!3DF8! y = \frac{{2x + 1}}{{x + 1}}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaiodaaeaacaaIXaGaeyOeI0Ia % amiEaaaaaaa!3D49! y = \frac{{x + 3}}{{1 - x}}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaikdaaeaacaWG4bGaey4kaSIa % aGymaaaaaaa!3D3D! y = \frac{{x + 2}}{{x + 1}}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgkHiTiaaigdaaeaacaWG4bGaey4kaSIa % aGymaaaaaaa!3D47! y = \frac{{x - 1}}{{x + 1}}\)
Câu 10:

Cho một cấp số cộng \(\ \left( {{u_n}} \right)\) có \({u_1} = \frac{1}{3} ; u_8 = 26\) , Tìm công sai \( d\)

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabg2 % da9maalaaabaGaaGymaiaaigdaaeaacaaIZaaaaaaa!3A26! d = \frac{{11}}{3}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabg2 % da9maalaaabaGaaGymaiaaicdaaeaacaaIZaaaaaaa!3A25! d = \frac{{10}}{3}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabg2 % da9maalaaabaGaaGymaiaaicdaaeaacaaIZaaaaaaa!3A25! d = \frac{{10}}{3}\)

C. \(d= \frac{3}{{10}}\)

D. \(d = \frac{3}{{11}}\)
Câu 11:

Đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaa % dIhacqGHRaWkcaaIXaaabaGaeyOeI0IaaGPaVlaaiwdacaWG4bWaaW % baaSqabeaacaaIYaaaaOGaeyOeI0IaaGOmaiaadIhacqGHRaWkcaaI % Zaaaaaaa!46E0 y = \frac{{{x^2} + x + 1}}{{ - \,5{x^2} - 2x + 3}}\) có bao nhiêu đường tiệm cận?

A. 4

B. 3

C. 2

D. 1
Câu 12:

Cho tứ diện đều \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaadk % eacaWGdbGaamiraaaa!3912! ABCD\) , \(M\) là trung điểm của cạnh \(BC\) . Khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4yaiaac+ % gacaGGZbWaaeWaaeaacaWGbbGaamOqaiaacYcacaWGebGaamytaaGa % ayjkaiaawMcaaaaa!3E28! \cos \left( {AB,DM} \right)\) bằng:

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaada % GcaaqaaiaaiodaaSqabaaakeaacaaI2aaaaaaa!37A6! \frac{{\sqrt 3 }}{6}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaada % GcaaqaaiaaikdaaSqabaaakeaacaaIYaaaaaaa!37A1! \frac{{\sqrt 2 }}{2}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaada % GcaaqaaiaaiodaaSqabaaakeaacaaIYaaaaaaa!37A2! \frac{{\sqrt 3 }}{2}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGOmaaaaaaa!377B! \frac{1}{2}\)
Câu 13:

Trong các hàm số sau, hàm số nào đồng biến trên \(R\) .

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaisdaaaGccqGHRaWkcaWG4bWaaWba % aSqabeaacaaIYaaaaOGaey4kaSIaaGymaaaa!3E59! y = {x^4} + {x^2} + 1\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHRaWkcaaIXaaaaa!3B86! y = {x^3} + 1\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGinaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiab % gUcaRiaaikdaaaaaaa!3DFB! y = \frac{{4x + 1}}{{x + 2}}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iGacshacaGGHbGaaiOBaiaadIhaaaa!3BC6! y = \tan x\)
Câu 14:

Cho hình chóp \(S.ABCD\)có đáy \(ABCD\) là hình vuông cạnh \(a\) . Biết \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadg % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaiaadseaaiaawIca % caGLPaaaaaa!3DEA! SA \bot \left( {ABCD} \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadg % eacqGH9aqpcaWGHbWaaOaaaeaacaaIZaaaleqaaaaa!3A56! SA = a\sqrt 3 \). Thể tích của khối chóp \(S.ABCD\)là:

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaCa % aaleqabaGaaG4maaaakmaakaaabaGaaG4maaWcbeaaaaa!38A6! {a^3}\sqrt 3 \)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOWaaOaaaeaacaaIZaaaleqaaaGc % baGaaGymaiaaikdaaaaaaa!3A37! \frac{{{a^3}\sqrt 3 }}{{12}}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOWaaOaaaeaacaaIZaaaleqaaaGc % baGaaG4maaaaaaa!397D! \frac{{{a^3}\sqrt 3 }}{3}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaaGcbaGaaGinaaaaaaa!389C! \frac{{{a^3}}}{4}\)
Câu 15:

Chọn kết quả đúng của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisP % aeqaaOWaaSaaaeaacaaIXaGaey4kaSIaaG4maiaadIhaaeaadaGcaa % qaaiaaikdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaG4m % aaWcbeaaaaaaaa!4611! \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + 3x}}{{\sqrt {2{x^2} + 3} }}\) .

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0YaaS % aaaeaacaaIZaWaaOaaaeaacaaIYaaaleqaaaGcbaGaaGOmaaaaaaa!394B! - \frac{{3\sqrt 2 }}{2}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0YaaS % aaaeaacaaIZaWaaOaaaeaacaaIYaaaleqaaaGcbaGaaGOmaaaaaaa!394B! - \frac{{\sqrt 2 }}{2}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0YaaS % aaaeaacaaIZaWaaOaaaeaacaaIYaaaleqaaaGcbaGaaGOmaaaaaaa!394B! \frac{{3\sqrt 2 }}{2}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0YaaS % aaaeaacaaIZaWaaOaaaeaacaaIYaaaleqaaaGcbaGaaGOmaaaaaaa!394B! \frac{{\sqrt 2 }}{2}\)
Câu 16:

Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ?

A. 0

B. 2

C. Vô số

D. 1
Câu 17:

Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích là \(V\), thể tích của khối chóp \(C'.ABC\) là:

A. 2V

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGOmaaaacaWGwbaaaa!3856! \frac{1}{2}V\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGOmaaaacaWGwbaaaa!3856! \frac{1}{3}V\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGOmaaaacaWGwbaaaa!3856! \frac{1}{6}V\)
Câu 18:

Công thức tính số tổ hợp là:

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaDa % aaleaacaWGUbaabaGaam4Aaaaakiabg2da9maalaaabaGaamOBaiaa % cgcaaeaadaqadaqaaiaad6gacqGHsislcaWGRbaacaGLOaGaayzkaa % Gaaiyiaaaaaaa!4081! C_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaDa % aaleaacaWGUbaabaGaam4Aaaaakiabg2da9maalaaabaGaamOBaiaa % cgcaaeaadaqadaqaaiaad6gacqGHsislcaWGRbaacaGLOaGaayzkaa % GaaiyiaiaadUgacaGGHaaaaaaa!4216! C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaWGUbaabaGaam4Aaaaakiabg2da9maalaaabaGaamOBaiaa % cgcaaeaadaqadaqaaiaad6gacqGHsislcaWGRbaacaGLOaGaayzkaa % Gaaiyiaaaaaaa!407F! A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaWGUbaabaGaam4Aaaaakiabg2da9maalaaabaGaamOBaiaa % cgcaaeaadaqadaqaaiaad6gacqGHsislcaWGRbaacaGLOaGaayzkaa % GaaiyiaiaadUgacaGGHaaaaaaa!4214! A_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\)
Câu 19:

Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaadk % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D0F! AB \bot \left( {ABC} \right)\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaado % eacqGHLkIxcaWGcbGaam4qaaaa!3AC1! AC \bot BC\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qaiaads % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaamiraaGaayjkaiaawMca % aaaa!3D14! CD \bot \left( {ABD} \right)\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqaiaado % eacqGHLkIxcaWGbbGaamiraaaa!3AC2! BC \bot AD\)
Câu 20:

Số mặt phẳng đối xứng của hình lập phương là:

A. 6

B. 7

C. 8

D. 9
Câu 21:

Thể tích của khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h là:

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbiqaaqugcaWGwb % Gaeyypa0JaamOqaiaadIgaaaa!39E9! V = Bh\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbiqaaqugcaWGwb % Gaeyypa0ZaaSaaaeaacaaIXaaabaGaaG4maaaacaWGcbGaamiAaaaa % !3B71! V = \frac{1}{3}Bh\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvaiabg2 % da9maalaaabaGaaGymaaqaaiaaikdaaaGaamOqaiaadIgaaaa!3B10! V = \frac{1}{2}Bh\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbiqaaqugcaWGwb % Gaeyypa0ZaaSaaaeaacaaI0aaabaGaaG4maaaacaWGcbGaamiAaaaa % !3B74! V = \frac{4}{3}Bh\)
Câu 22:

Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maaceaabaqbaeaabiWa % aaqaamaalaaabaWaaOaaaeaacaaIYaGaamiEaiabgUcaRiaaiIdaaS % qabaGccqGHsislcaaIYaaabaWaaOaaaeaacaWG4bGaey4kaSIaaGOm % aaWcbeaaaaaakeaacaqGRbGaaeiAaiaabMgaaeaacaWG4bGaeyOpa4 % JaeyOeI0IaaGOmaaqaaiaaicdaaeaacaqGRbGaaeiAaiaabMgaaeaa % caWG4bGaeyypa0JaeyOeI0IaaGOmaaaaaiaawUhaaaaa!512F! f\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{\sqrt {2x + 8} - 2}}{{\sqrt {x + 2} }}}&{{\rm{khi}}}&{x > - 2}\\ 0&{{\rm{khi}}}&{x = - 2} \end{array}} \right.\) . Tìm khẳng định đúng trong các khẳng định sau:

\((I)\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaqadaqaaiabgkHi % TiaaikdaaiaawIcacaGLPaaadaahaaadbeqaaiabgUcaRaaaaSqaba % GccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0JaaGim % aaaa!456E! \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = 0\) .

\((II)\) \(f(x)\) liên tục tại \(x=-2\).

\((III)\) \(f(x)\) gián đoạn tại \(x=-2\).

A. Chỉ (III)

B. Chỉ (I)

C. Chỉ (I) và (II)

D. Chỉ (I) và (III)
Câu 23:

Khẳng định nào sau đây đúng:

A. Nếu hai mặt phẳng (P) và (Q) lần lượt chứa hai đường thẳng song song thì song song với nhau.

B. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mọi đường thẳng nằm trên mặt phẳng kia.

C. Hai mặt phẳng phân biệt không song song thì cắt nhau.

D. Hai mặt phẳng cùng song song với một đường thẳng thì song song với nhau.
Câu 24:

Cho khối chóp S.ABC , trên ba cạnh SA,SB, SC lần lượt lấy ba điểm A' ,B' ,C' sao cho \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiqadg % eagaqbaiabg2da9maalaaabaGaaGymaaqaaiaaikdaaaGaam4uaiaa % dgeaaaa!3BC8! SA' = \frac{1}{2}SA\) ,\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiqadk % eagaqbaiabg2da9maalaaabaGaaGymaaqaaiaaiodaaaGaam4uaiaa % dkeaaaa!3BCB! SB' = \frac{1}{3}SB\) ,\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiqado % eagaqbaiabg2da9maalaaabaGaaGymaaqaaiaaisdaaaGaam4uaiaa % doeaaaa!3BCE! SC' = \frac{1}{4}SC\) . Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C' . Khi đó tỉ số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaace % WGwbGbauaaaeaacaWGwbaaaaaa!37C5! \frac{{V'}}{V}\) là:

A. 12

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGymaiaaikdaaaaaaa!3835! \frac{1}{{12}}\)

C. 24

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGymaiaaikdaaaaaaa!3835! \frac{1}{{24}}\)
Câu 25:

Nghiệm của phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaWGUbaabaGaaG4maaaakiabg2da9iaaikdacaaIWaGaamOB % aaaa!3C0F! A_n^3 = 20n\) là:

A. n = 6

B. n = 5

C. n = 8

D. Không tồn tại
Câu 26:

Cho hàm số \(y=sin2x\) . Khẳng định nào sau đây là đúng?

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaCa % aaleqabaGaaGOmaaaakiabgkHiTmaabmaabaGabmyEayaafaaacaGL % OaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaeyypa0JaaGinaaaa!3E1C! {y^2} - {\left( {y'} \right)^2} = 4\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGinaiaadM % hacqGHRaWkceWG5bGbauGbauaacqGH9aqpcaaIWaaaaa!3B67! 4y + y'' = 0\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGinaiaadM % hacqGHsislceWG5bGbauGbauaacqGH9aqpcaaIWaaaaa!3B72! 4y - y'' = 0\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iqadMhagaqbaiaac6caciGG0bGaaiyyaiaac6gacaaIYaGaamiE % aaaa!3E3E! y = y'.\tan 2x\)
Câu 27:

Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiEamaa % CaaaleqabaGaaGOmaaaakiabgUcaRiaadIhacqGHRaWkcaaIXaaaba % GaamiEaiabgUcaRiaaigdaaaaaaa!4281! f\left( x \right) = \frac{{{x^2} + x + 1}}{{x + 1}}\) có bao nhiêu điểm cực trị?

A. 3

B. 2

C. 1

D. 0
Câu 28:

Đồ thị sau đây là của hàm số nào?

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaadIhadaahaaWcbeqaaiaaisdaaaGccqGHRaWkcaaI % 0aGaamiEamaaCaaaleqabaGaaGOmaaaaaaa!3E5D! y = - {x^4} + 4{x^2}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaadIhadaahaaWcbeqaaiaaisdaaaGccqGHsislcaaI % YaGaamiEamaaCaaaleqabaGaaGOmaaaaaaa!3E66! y = - {x^4} - 2{x^2}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTmaalaaabaGaaGymaaqaaiaaisdaaaGaamiEamaaCaaa % leqabaGaaGinaaaakiabgUcaRiaaiodacaWG4bWaaWbaaSqabeaaca % aIYaaaaaaa!3FE4! y = - \frac{1}{4}{x^4} + 3{x^2}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaisdaaaGccqGHsislcaaIZaGaamiE % amaaCaaaleqabaGaaGOmaaaaaaa!3D7A! y = {x^4} - 3{x^2}\)
Câu 29:

Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B. Vẽ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D28! SH \bot \left( {ABC} \right)\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamisaiabgI % GiopaabmaabaGaamyqaiaadkeacaWGdbaacaGLOaGaayzkaaaaaa!3C23! H \in \left( {ABC} \right)\) . Khẳng định nào sau đây đúng?

A. H trùng với trực tâm tam giác ABC

B. H trùng với trọng tâm tam giác ABC.

C. H trùng với trung điểm AC.

D. H trùng với trung điểm BC.
Câu 30:

Trong khai triển \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WG4bGaey4kaSYaaSaaaeaacaaIYaaabaWaaOqaaeaacaWG4baaleaa % aaaaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaI2aaaaaaa!3C37! {\left( {x + \frac{2}{{\sqrt[{}]{x}}}} \right)^6}\), hệ số của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaG4maaaakiaacYcaaaa!3895! {x^3},\) \((x>0)\) là:

A. 60

B. 80

C. 160

D. 240
Câu 31:

Cho khối lăng trụ đứng tam giác ABC.A'B'C' có đáy là một tam giác vuông cân tại A , AC =AB= 2a , góc giữa AC' và mặt phẳng (ABC) bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaG4maiaaic % dacqGHWcaSaaa!3957! 30^\circ \). Thể tích khối lăng trụ ABC.A'B'C' là

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aI0aGaamyyamaakaaabaGaaG4maaWcbeaaaOqaaiaaiodaaaaaaa!3947! \frac{{4a\sqrt 3 }}{3}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aI0aGaamyyamaaCaaaleqabaGaaG4maaaakmaakaaabaGaaG4maaWc % beaaaOqaaiaaiodaaaaaaa!3A3B! \frac{{4{a^3}\sqrt 3 }}{3}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIYaGaamyyamaaCaaaleqabaGaaG4maaaakmaakaaabaGaaG4maaWc % beaaaOqaaiaaiodaaaaaaa!3A39! \frac{{2{a^3}\sqrt 3 }}{3}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aI0aGaamyyamaaCaaaleqabaGaaGOmaaaakmaakaaabaGaaG4maaWc % beaaaOqaaiaaiodaaaaaaa!3A3A! \frac{{4{a^2}\sqrt 3 }}{3}\)
Câu 32:

Đồ thị sau đây là của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaisdaaaGccqGHsislcaaIZaGaamiE % amaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiodaaaa!3F2D! y = {x^4} - 3{x^2} - 3\). Với giá trị nào của m thì phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGinaaaakiabgkHiTiaaiodacaWG4bWaaWbaaSqabeaa % caaIYaaaaOGaey4kaSIaamyBaiabg2da9iaaicdaaaa!3F13! {x^4} - 3{x^2} + m = 0\) có ba nghiệm phân biệt?

A. m = -3

B. m = -4

C. m = 0

D. m = 4
Câu 33:

Cho hàm số:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maabmaabaGaaGymaiabgkHiTiaad2gaaiaawIcacaGLPaaacaWG % 4bWaaWbaaSqabeaacaaI0aaaaOGaeyOeI0IaamyBaiaadIhadaahaa % WcbeqaaiaaikdaaaGccqGHRaWkcaaIYaGaamyBaiabgkHiTiaaigda % aaa!4614! y = \left( {1 - m} \right){x^4} - m{x^2} + 2m - 1\) . Tìm m để đồ thị hàm số có đúng một cực trị

A. \(m<0\)

B. \(m<0 \) hoặc \(m<-1\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgs % MiJkaaicdaaaa!3955! m \le 0\) hoặc \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgw % MiZkaaigdaaaa!3967! m \ge 1\)

D. \(m>1\)
Câu 34:

Tính giới hạn: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaacM % gacaGGTbWaamWaaeaadaqadaqaaiaaigdacqGHsisldaWcaaqaaiaa % igdaaeaacaaIYaWaaWbaaSqabeaacaaIYaaaaaaaaOGaayjkaiaawM % caamaabmaabaGaaGymaiabgkHiTmaalaaabaGaaGymaaqaaiaaioda % daahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaaiOlaiaac6 % cacaGGUaWaaeWaaeaacaaIXaGaeyOeI0YaaSaaaeaacaaIXaaabaGa % amOBamaaCaaaleqabaGaaGOmaaaaaaaakiaawIcacaGLPaaaaiaawU % facaGLDbaaaaa!4E05! \lim \left[ {\left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)...\left( {1 - \frac{1}{{{n^2}}}} \right)} \right]\) .

A. 1

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGOmaaaaaaa!377B! \frac{1}{2}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGOmaaaaaaa!377B! \frac{1}{4}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaaGOmaaaaaaa!377B! \frac{3}{2}\)
Câu 35:

Cho hàm số: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTmaalaaabaGaamiEamaaCaaaleqabaGaaG4maaaaaOqa % aiaaiodaaaGaey4kaSYaaeWaaeaacaWGHbGaeyOeI0IaaGymaaGaay % jkaiaawMcaaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkdaqa % daqaaiaadggacqGHRaWkcaaIZaaacaGLOaGaayzkaaGaamiEaiabgk % HiTiaaisdaaaa!4A24! y = - \frac{{{x^3}}}{3} + \left( {a - 1} \right){x^2} + \left( {a + 3} \right)x - 4\) . Tìm a để hàm số đồng biến trên khoảng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIWaGaai4oaiaaykW7caaMc8UaaG4maaGaayjkaiaawMcaaaaa!3CC9! \left( {0;\,\,3} \right)\)

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiabgw % MiZoaalaaabaGaaGymaiaaikdaaeaacaaI3aaaaaaa!3AE8! a \ge \frac{{12}}{7}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiabgY % da8iabgkHiTiaaiodaaaa!3988! a < - 3\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiabgs % MiJkabgkHiTiaaiodaaaa!3A39! a \le - 3\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiabg6 % da+maalaaabaGaaGymaiaaikdaaeaacaaI3aaaaaaa!3A2A! a > \frac{{12}}{7}\)
Câu 36:

Tìm m để phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiGaco % hacaGGPbGaaiOBamaaCaaaleqabaGaaGOmaaaakiaadIhacqGHRaWk % caWGTbGaaiOlaiGacohacaGGPbGaaiOBaiaaikdacaWG4bGaeyypa0 % JaaGOmaiaad2gaaaa!4542! 2{\sin ^2}x + m.\sin 2x = 2m\) vô nghiệm.

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgY % da8iaaicdacaGG7aaaaa!3962! m < 0;\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgw % MiZoaalaaabaGaaGinaaqaaiaaiodaaaaaaa!3A36! m \ge \frac{4}{3}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgs % MiJkaaicdacaGG7aaaaa!3A13! m \le 0;\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgw % MiZoaalaaabaGaaGinaaqaaiaaiodaaaaaaa!3A36! m \ge \frac{4}{3}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGimaiabgs % MiJkaad2gacqGHKjYOdaWcaaqaaiaaisdaaeaacaaIZaaaaaaa!3C94! 0 \le m \le \frac{4}{3}\)

D. \(m<0\) hoặc \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabg6 % da+maalaaabaGaaGinaaqaaiaaiodaaaaaaa!3978! m > \frac{4}{3}\)
Câu 37:

Một chất điểm chuyển động theo quy luật \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaabm % aabaGaamiDaaGaayjkaiaawMcaaiabg2da9iaaigdacqGHRaWkcaaI % ZaGaamiDamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaadshadaahaa % Wcbeqaaiaaiodaaaaaaa!4169! S\left( t \right) = 1 + 3{t^2} - {t^3}\) . Vận tốc của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu

A. 2

B. 1

C. 3

D. 4
Câu 38:

Cho đồ thị (C) của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maabmaabaGaaGymaiabgkHiTiaadIhaaiaawIcacaGLPaaadaqa % daqaaiaadIhacqGHRaWkcaaIYaaacaGLOaGaayzkaaWaaWbaaSqabe % aacaaIYaaaaaaa!4132! y = \left( {1 - x} \right){\left( {x + 2} \right)^2}\) . Trong các mệnh đề sau, tìm mệnh đề sai:

A. (C) có hai điểm cực trị.

B. (C) có một điểm uốn.

C. (C) có một tâm đối xứng.

D. (C) có một trục đối xứng.
Câu 39:

Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50.000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 40 quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 5000 đồng thì số bưởi bán được tăng thêm là 50 quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là 30.000 đồng.

A. 44.000 đ

B. 43.000 đ

C. 42.000 đ

D. 41.000 đ
Câu 40:

Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với đáy một góc \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOXdOgaaa!37B0! \varphi \) . Thể tích của khối chóp đó bằng

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOGaciiDaiaacggacaGGUbGaeqOX % dOgabaGaaGymaiaaikdaaaaaaa!3DE2! \frac{{{a^3}\tan \varphi }}{{12}}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOGaci4yaiaac+gacaGG0bGaeqOX % dOgabaGaaGymaiaaikdaaaaaaa!3DE5! \frac{{{a^3}\cot \varphi }}{{12}}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOGaciiDaiaacggacaGGUbGaeqOX % dOgabaGaaGOnaaaaaaa!3D2B! \frac{{{a^3}\tan \varphi }}{6}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOGaci4yaiaac+gacaGG0bGaeqOX % dOgabaGaaGOnaaaaaaa!3D2E! \frac{{{a^3}\cot \varphi }}{6}\)
Câu 41:

Cho hình chóp S.ABC có đáy là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqKaam % yqaiaadkeacaWGdbaaaa!39AE! \Delta ABC\) vuông cân ở B, \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaado % eacqGH9aqpcaWGHbWaaOaaaeaacaaIYaaaleqaaOGaaiilaiaaykW7 % aaa!3C89! AC = a\sqrt 2 ,\,\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadg % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aiaacYcaaaa!3DD0! SA \bot \left( {ABC} \right),\) SA = a. Gọi G là trọng tâm của \(\Delta SBC\) , \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiaadc % hadaqadaqaaiabeg7aHbGaayjkaiaawMcaaaaa!3B02! mp\left( \alpha \right)\) đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S. Tính V

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aI0aGaamyyamaaCaaaleqabaGaaG4maaaaaOqaaiaaiMdaaaGaaiOl % aaaa!3A10! \frac{{4{a^3}}}{9}.\)

B. \(\frac{{4{a^3}}}{27}.\)

C. \(\frac{{5{a^3}}}{54}.\)

D. \(\frac{{2{a^3}}}{9}.\)
Câu 42:

Cho hình chóp đều S.ABC có cạnh đáy bằng a , góc giữa một mặt bên và mặt đáy bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOnaiaaic % dacqGHWcaSaaa!395A! 60^\circ \) . Tính độ dài đường cao SH.

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaikdaaSqabaaakeaa % caaIZaaaaiaac6caaaa!3BE4! SH = \frac{{a\sqrt 2 }}{3}.\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaiodaaSqabaaakeaa % caaIYaaaaiaac6caaaa!3BE4! SH = \frac{{a\sqrt 3 }}{2}.\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGH9aqpdaWcaaqaaiaadggaaeaacaaIYaaaaiaac6caaaa!3B02! SH = \frac{a}{2}.\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaiodaaSqabaaakeaa % caaIZaaaaiaac6caaaa!3BE5! SH = \frac{{a\sqrt 3 }}{3}.\)
Câu 43:

Tìm m để phương trình sau có nghiệm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaada % GcaaqaaiaaisdacqGHsislcaWG4baaleqaaOGaey4kaSYaaOaaaeaa % caaI0aGaey4kaSIaamiEaaWcbeaaaOGaayjkaiaawMcaamaaCaaale % qabaGaaG4maaaakiabgkHiTiaaiAdadaGcaaqaaiaaigdacaaI2aGa % eyOeI0IaamiEamaaCaaaleqabaGaaGOmaaaaaeqaaOGaey4kaSIaaG % Omaiaad2gacqGHRaWkcaaIXaGaeyypa0JaaGimaiaac6caaaa!4B96! {\left( {\sqrt {4 - x} + \sqrt {4 + x} } \right)^3} - 6\sqrt {16 - {x^2}} + 2m + 1 = 0.\)

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgI % Giolabl2riHkaac6caaaa!3A8C! m \in R .\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabg6 % da+maalaaabaGaeyOeI0IaaGymaiabgkHiTiaaigdacaaI2aWaaOaa % aeaacaaIYaaaleqaaaGcbaGaaGOmaaaacaGGUaaaaa!3E5D! m > \frac{{ - 1 - 16\sqrt 2 }}{2}.\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0YaaS % aaaeaacaaI0aGaaGymaaqaaiaaikdaaaGaeyizImQaamyBaiabgsMi % JoaalaaabaGaeyOeI0IaaGymaiabgkHiTiaaigdacaaI2aWaaOaaae % aacaaIYaaaleqaaaGcbaGaaGOmaaaacaGGUaaaaa!43F1! - \frac{{41}}{2} \le m \le \frac{{ - 1 - 16\sqrt 2 }}{2}.\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgY % da8iabgkHiTmaalaaabaGaaGinaiaaigdaaeaacaaIYaaaaiaac6ca % aaa!3BCE! m < - \frac{{41}}{2}.\)
Câu 44:

Tìm nghiệm của phương trình \( {\sin ^2}x + \sin x = 0\) thỏa mãn điều kiện \( - \frac{\pi }{2} < x < \frac{\pi }{2}.\)

A. \( x = \frac{\pi }{2}.\)

B. \(x=0\)

C. \( x= \pi .\)

D. \( x = \frac{\pi }{3}.\)
Câu 45:

Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(m) của mực nước trong kênh tính theo thời gian t(h) được cho bởi công thức: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2 % da9iaaiodaciGGJbGaai4BaiaacohadaqadaqaamaalaaabaGaeqiW % daNaamiDaaqaaiaaiAdaaaGaey4kaSYaaSaaaeaacqaHapaCaeaaca % aIZaaaaaGaayjkaiaawMcaaiabgUcaRiaaigdacaaIYaaaaa!464B! h = 3\cos \left( {\frac{{\pi t}}{6} + \frac{\pi }{3}} \right) + 12\)

Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?

A. t =22(h)

B. t =15(h)

C. t =14(h)

D. t = 10(h)
Câu 46:

Cho lăng trụ đứng tam giác ABC.A'BC' có đáy là một tam giác vuông cân tại B, AB = BC = a,\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiqadg % eagaqbaiabg2da9iaadggadaGcaaqaaiaaikdaaSqabaaaaa!3A4F! AA' = a\sqrt 2\) , M là trung điểm BC . Tính khoảng cách giữa hai đường thẳng AM và B'C.

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbaabaWaaOaaaeaacaaI3aaaleqaaaaaaaa!37C6! \frac{a}{{\sqrt 7 }}\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaOaaaeaacaaIZaaaleqaaaGcbaGaaGOmaaaaaaa!3888! \frac{{a\sqrt 3 }}{2}\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIYaGaamyyaaqaamaakaaabaGaaGynaaWcbeaaaaaaaa!3880! \frac{{2a}}{{\sqrt 5 }}\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaka % aabaGaaG4maaWcbeaaaaa!37B2! a\sqrt 3 \)
Câu 47:

Có bao nhiêu số tự nhiên có sáu chữ số khác nhau từng đôi một, trong đó chữ số 5 đứng liền giữa hai chữ số 1 và 4 ?

A. 249

B. 1500

C. 3204

D. 2942
Câu 48:

Cho lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaOaaaeaacaaIZaaaleqaaaGcbaGaaGinaaaaaaa!388A! \frac{{a\sqrt 3 }}{4}\). Khi đó thể tích của khối lăng trụ là

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOWaaOaaaeaacaaIZaaaleqaaaGc % baGaaGymaiaaikdaaaGaaiOlaaaa!3AE9! \frac{{{a^3}\sqrt 3 }}{{12}}.\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOWaaOaaaeaacaaIZaaaleqaaaGc % baGaaGOnaaaacaGGUaaaaa!3A32! \frac{{{a^3}\sqrt 3 }}{6}.\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOWaaOaaaeaacaaIZaaaleqaaaGc % baGaaG4maaaacaGGUaaaaa!3A2F! \frac{{{a^3}\sqrt 3 }}{3}.\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOWaaOaaaeaacaaIZaaaleqaaaGc % baGaaGOmaiaaisdaaaGaaiOlaaaa!3AEC! \frac{{{a^3}\sqrt 3 }}{{24}}.\)
Câu 49:

Anh Minh muốn xây dựng một hố ga không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được \(3200cm^3\) , tỉ số giữa chiều cao và chiều rộng của hố ga bằng 2 . Xác định diện tích đáy của hố ga để khi xây hố tiết kiệm được nguyên vật liệu nhất.

A. \(170cm^2\)

B. \(160cm^2\)

C. \(150cm^2\)

D. \(140cm^2\)
Câu 50:

Trong mặt phẳng Oxy , tìm phương trình đường tròn (C') là ảnh của đường tròn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGdbaacaGLOaGaayzkaaGaaiOoaiaadIhadaahaaWcbeqaaiaaikda % aaGccqGHRaWkcaWG5bWaaWbaaSqabeaacaaIYaaaaOGaeyypa0JaaG % ymaaaa!3F87! \left( C \right):{x^2} + {y^2} = 1\) qua phép đối xứng tâm I( 1; 0) .

A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WG4bGaey4kaSIaaGOmaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOm % aaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikdaaaGccqGH9aqpca % aIXaaaaa!3F9F! {\left( {x + 2} \right)^2} + {y^2} = 1\)

B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgUcaRmaabmaabaGaamyEaiabgUcaRiaa % ikdaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGH9aqpca % aIXaaaaa!3F9F! {x^2} + {\left( {y + 2} \right)^2} = 1\)

C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WG4bGaeyOeI0IaaGOmaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOm % aaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikdaaaGccqGH9aqpca % aIXaaaaa!3FAA! {\left( {x - 2} \right)^2} + {y^2} = 1\)

D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgUcaRmaabmaabaGaamyEaiabgkHiTiaa % ikdaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGH9aqpca % aIXaaaaa!3FAA! {x^2} + {\left( {y - 2} \right)^2} = 1\)

Top 10/9 lượt thi

Bạn có muốn chinh phục đề thi này

Có, tôi muốn!

TÀI LIỆU THAM KHẢO

Lý thuyết Công Nghệ lớp 12 đầy đủ và chi tiết

Lý thuyết Tin Học lớp 12 đầy đủ và chi tiết

Lý thuyết Hoá học lớp 12 theo chuyên đề và bài học

Lý thuyết Vật lý lớp 12 theo chuyên đề và bài học

Bài giảng Đia lý lớp 12 hệ thống hoá kiến thức tốt nhất

Lý thuyết Giải tích và Hinh học lớp 12 đầy đủ và chi tiết

Hướng dẫn giải SGK, SBT và nâng cao Toán 12

Hướng dẫn giải SGK, SBT và nâng cao Hoá học 12

Hướng dẫn giải SGK, SBT và nâng cao Vật lý 12

Soạn văn lớp 12 Tập 1 và Tập 2 siêu ngắn và hay nhất

Bài giảng Lịch Sử lớp 12 hệ thống hoá kiến thức tốt nhất

Hướng dẫn giải bài Tiếng Anh và Tiếng Anh mới 12

Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020

Câu 1:

Câu 2:

Câu 3:

Một tổ học sinh có nam và nữ. Chọn ngẫu nhiên người. Tính xác suất sao cho người được chọn đều là nữ.

Câu 4:

Câu 5:

Câu 6:

Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

Câu 7:

Câu 8:

Câu 9:

Đồ thị sau đây là của hàm số nào?

Câu 10:

Cho một cấp số cộng \(\ \left( {{u_n}} \right)\) có \({u_1} = \frac{1}{3} ; u_8 = 26\) , Tìm công sai \( d\)

Câu 11:

Câu 12:

Câu 13:

Trong các hàm số sau, hàm số nào đồng biến trên \(R\) .

Câu 14:

Câu 15:

Câu 16:

Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ?

Câu 17:

Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích là \(V\), thể tích của khối chóp \(C'.ABC\) là:

Câu 18:

Công thức tính số tổ hợp là:

Câu 19:

Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?

Câu 20:

Số mặt phẳng đối xứng của hình lập phương là:

Câu 21:

Thể tích của khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h là:

Câu 22:

Câu 23:

Khẳng định nào sau đây đúng:

Câu 24:

Câu 25:

Câu 26:

Cho hàm số \(y=sin2x\) . Khẳng định nào sau đây là đúng?

Câu 27:

Câu 28:

Đồ thị sau đây là của hàm số nào?

Câu 29:

Câu 30:

Câu 31:

Câu 32:

Câu 33:

Câu 34:

Câu 35:

Câu 36:

Câu 37:

Câu 38:

Câu 39:

Câu 40:

Câu 41:

Câu 42:

Câu 43:

Câu 44:

Tìm nghiệm của phương trình \( {\sin ^2}x + \sin x = 0\) thỏa mãn điều kiện \( - \frac{\pi }{2} < x < \frac{\pi }{2}.\)

Câu 45:

Câu 46:

Câu 47:

Có bao nhiêu số tự nhiên có sáu chữ số khác nhau từng đôi một, trong đó chữ số 5 đứng liền giữa hai chữ số 1 và 4 ?

Câu 48:

Câu 49:

Câu 50:

Đề thi liên quan

Đề thi giữa HK2 môn Toán 6 CD năm 2023-2024

Đề thi giữa HK2 môn Toán 6 CTST năm 2023-2024

Đề thi giữa HK2 môn Toán 6 KNTT năm 2023-2024

TÀI LIỆU THAM KHẢO