Cho khối lăng trụ đứng tam giác ABC.A'B'C' có đáy là một tam giác vuông cân tại A , AC =AB= 2a , góc giữa AC' và mặt phẳng (ABC) bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaG4maiaaic % dacqGHWcaSaaa!3957! 30^\circ \). Thể tích khối lăng trụ ABC.A'B'C' là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai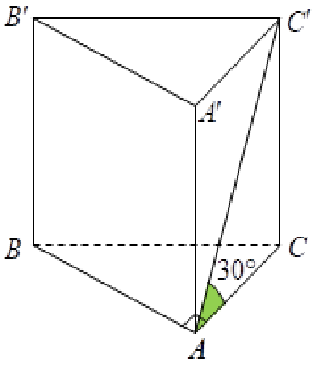
Ta có AC là hình chiếu vuông góc của AC' lên mặt phẳng (ABC)
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aae % WaaeaadaqiaaqaaiaadgeaceWGdbGbauaacaGGSaGaaGPaVpaabmaa % baGaamyqaiaadkeacaWGdbaacaGLOaGaayzkaaaacaGLcmaaaiaawI % cacaGLPaaacqGH9aqpdaqiaaqaaiaadoeacaWGbbGabm4qayaafaaa % caGLcmaacqGH9aqpcaaIZaGaaGimaiabgclaWcaa!4AE2! \Rightarrow \left( {\widehat {AC',\,\left( {ABC} \right)}} \right) = \widehat {CAC'} = 30^\circ \)
Tam giác ACC' vuông tại C có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qaiqado % eagaqbaiabg2da9iaadgeacaWGdbGaaiOlaiGacshacaGGHbGaaiOB % aiaaiodacaaIWaGaeyiSaaRaeyypa0ZaaSaaaeaacaaIYaGaamyyam % aakaaabaGaaG4maaWcbeaaaOqaaiaaiodaaaaaaa!4561! CC' = AC.\tan 30^\circ = \frac{{2a\sqrt 3 }}{3}\)
Khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaaBa % aaleaacaWGbbGaamOqaiaadoeacaGGUaGabmyqayaafaGabmOqayaa % faGabm4qayaafaaabeaakiabg2da9iaadofadaWgaaWcbaGaamyqai % aadkeacaWGdbaabeaakiaac6cacaWGdbGabm4qayaafaGaeyypa0Za % aSaaaeaacaaI0aGaamyyamaaCaaaleqabaGaaG4maaaakmaakaaaba % GaaG4maaWcbeaaaOqaaiaaiodaaaaaaa!4889! {V_{ABC.A'B'C'}} = {S_{ABC}}.CC' = \frac{{4{a^3}\sqrt 3 }}{3}\)
Câu hỏi liên quan
-
Cho đồ thị (C) của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maabmaabaGaaGymaiabgkHiTiaadIhaaiaawIcacaGLPaaadaqa % daqaaiaadIhacqGHRaWkcaaIYaaacaGLOaGaayzkaaWaaWbaaSqabe % aacaaIYaaaaaaa!4132! y = \left( {1 - x} \right){\left( {x + 2} \right)^2}\) . Trong các mệnh đề sau, tìm mệnh đề sai:
-
Đồ thị sau đây là của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaisdaaaGccqGHsislcaaIZaGaamiE % amaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiodaaaa!3F2D! y = {x^4} - 3{x^2} - 3\). Với giá trị nào của m thì phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGinaaaakiabgkHiTiaaiodacaWG4bWaaWbaaSqabeaa % caaIYaaaaOGaey4kaSIaamyBaiabg2da9iaaicdaaaa!3F13! {x^4} - 3{x^2} + m = 0\) có ba nghiệm phân biệt?
.png)
-
Khẳng định nào sau đây đúng:
-
Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(m) của mực nước trong kênh tính theo thời gian t(h) được cho bởi công thức: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2 % da9iaaiodaciGGJbGaai4BaiaacohadaqadaqaamaalaaabaGaeqiW % daNaamiDaaqaaiaaiAdaaaGaey4kaSYaaSaaaeaacqaHapaCaeaaca % aIZaaaaaGaayjkaiaawMcaaiabgUcaRiaaigdacaaIYaaaaa!464B! h = 3\cos \left( {\frac{{\pi t}}{6} + \frac{\pi }{3}} \right) + 12\)
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
-
Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B. Vẽ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D28! SH \bot \left( {ABC} \right)\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamisaiabgI % GiopaabmaabaGaamyqaiaadkeacaWGdbaacaGLOaGaayzkaaaaaa!3C23! H \in \left( {ABC} \right)\) . Khẳng định nào sau đây đúng?
-
Cho lăng trụ đứng tam giác ABC.A'BC' có đáy là một tam giác vuông cân tại B, AB = BC = a,\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiqadg % eagaqbaiabg2da9iaadggadaGcaaqaaiaaikdaaSqabaaaaa!3A4F! AA' = a\sqrt 2\) , M là trung điểm BC . Tính khoảng cách giữa hai đường thẳng AM và B'C.
-
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maaceaabaqbaeaabiWa % aaqaamaalaaabaWaaOaaaeaacaaIYaGaamiEaiabgUcaRiaaiIdaaS % qabaGccqGHsislcaaIYaaabaWaaOaaaeaacaWG4bGaey4kaSIaaGOm % aaWcbeaaaaaakeaacaqGRbGaaeiAaiaabMgaaeaacaWG4bGaeyOpa4 % JaeyOeI0IaaGOmaaqaaiaaicdaaeaacaqGRbGaaeiAaiaabMgaaeaa % caWG4bGaeyypa0JaeyOeI0IaaGOmaaaaaiaawUhaaaaa!512F! f\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{\sqrt {2x + 8} - 2}}{{\sqrt {x + 2} }}}&{{\rm{khi}}}&{x > - 2}\\ 0&{{\rm{khi}}}&{x = - 2} \end{array}} \right.\) . Tìm khẳng định đúng trong các khẳng định sau:
\((I)\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaqadaqaaiabgkHi % TiaaikdaaiaawIcacaGLPaaadaahaaadbeqaaiabgUcaRaaaaSqaba % GccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0JaaGim % aaaa!456E! \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = 0\) .
\((II)\) \(f(x)\) liên tục tại \(x=-2\).
\((III)\) \(f(x)\) gián đoạn tại \(x=-2\).
-
Tính giới hạn: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaacM % gacaGGTbWaamWaaeaadaqadaqaaiaaigdacqGHsisldaWcaaqaaiaa % igdaaeaacaaIYaWaaWbaaSqabeaacaaIYaaaaaaaaOGaayjkaiaawM % caamaabmaabaGaaGymaiabgkHiTmaalaaabaGaaGymaaqaaiaaioda % daahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaaiOlaiaac6 % cacaGGUaWaaeWaaeaacaaIXaGaeyOeI0YaaSaaaeaacaaIXaaabaGa % amOBamaaCaaaleqabaGaaGOmaaaaaaaakiaawIcacaGLPaaaaiaawU % facaGLDbaaaaa!4E05! \lim \left[ {\left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)...\left( {1 - \frac{1}{{{n^2}}}} \right)} \right]\) .
-
Cho lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbWaaOaaaeaacaaIZaaaleqaaaGcbaGaaGinaaaaaaa!388A! \frac{{a\sqrt 3 }}{4}\). Khi đó thể tích của khối lăng trụ là
-
Cho một cấp số cộng \(\ \left( {{u_n}} \right)\) có \({u_1} = \frac{1}{3} ; u_8 = 26\) , Tìm công sai \( d\)
-
Một chất điểm chuyển động theo quy luật \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaabm % aabaGaamiDaaGaayjkaiaawMcaaiabg2da9iaaigdacqGHRaWkcaaI % ZaGaamiDamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaadshadaahaa % Wcbeqaaiaaiodaaaaaaa!4169! S\left( t \right) = 1 + 3{t^2} - {t^3}\) . Vận tốc của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu
-
Công thức tính số tổ hợp là:
-
Nghiệm của phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qaciGGJbGaai4BaiaacohacaWG4bGaeyypa0JaeyOeI0IaaGPaVlaa % cckadaWcaaqaaiaaigdaaeaacaaIYaaaaaaa!400C! \cos x = - \,\;\frac{1}{2}\) là :
-
Cho hàm số:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maabmaabaGaaGymaiabgkHiTiaad2gaaiaawIcacaGLPaaacaWG % 4bWaaWbaaSqabeaacaaI0aaaaOGaeyOeI0IaamyBaiaadIhadaahaa % WcbeqaaiaaikdaaaGccqGHRaWkcaaIYaGaamyBaiabgkHiTiaaigda % aaa!4614! y = \left( {1 - m} \right){x^4} - m{x^2} + 2m - 1\) . Tìm m để đồ thị hàm số có đúng một cực trị
-
Có bao nhiêu số tự nhiên có sáu chữ số khác nhau từng đôi một, trong đó chữ số 5 đứng liền giữa hai chữ số 1 và 4 ?
-
Cho hình chóp \(S.ABCD\)có đáy \(ABCD\) là hình vuông cạnh \(a\) . Biết \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadg % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaiaadseaaiaawIca % caGLPaaaaaa!3DEA! SA \bot \left( {ABCD} \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadg % eacqGH9aqpcaWGHbWaaOaaaeaacaaIZaaaleqaaaaa!3A56! SA = a\sqrt 3 \). Thể tích của khối chóp \(S.ABCD\)là:
-
Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích là \(V\), thể tích của khối chóp \(C'.ABC\) là:
-
Số mặt phẳng đối xứng của hình lập phương là:
-
Cho hàm số \(y=sin2x\) . Khẳng định nào sau đây là đúng?
-
Nghiệm của phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaWGUbaabaGaaG4maaaakiabg2da9iaaikdacaaIWaGaamOB % aaaa!3C0F! A_n^3 = 20n\) là:
