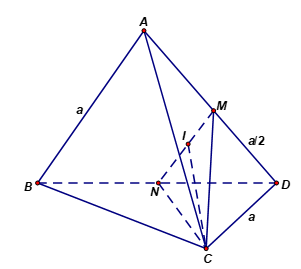
Cho hình tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M\) là trung điểm của cạnh \(AD\). Tính khoảng cách giữa 2 đường thẳng \(AB\) và \(CM\) theo \(a\)?

Nghiệm của phương trình sau \({{\log }_{2}}\left( x-1 \right)=4\) là?

Trong không gian \(Oxyz\) cho mặt cầu \((S):(x+2)^{2}+y^{2}+(z+5)^{2}=24\) cắt mp \((\alpha): x+y+4=0\) theo giao tuyến là đường tròn \((C)\). Điểm \(M\) thuộc \((C)\) sao cho khoàng cách từ \(M\) đến \(A(4 ;-12 ; 1)\) nhỏ nhất có tung độ bằng?

Cho hàm số \(y=f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và dấu của đạo hàm cho bởi công thức sau:

Hàm số \(f\left( x \right)\) có mấy điểm cực trị?

Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mp \(\left( ABC \right)\), \(SA=1\) và đáy \(ABC\) là tam giác đều với độ dài cạnh bằng 2. Tính góc giữa mặt phẳng \(\left( SBC \right)\) và mặt phẳng \(\left( ABC \right)\)?

Biết rằng đồ thị \((H):y=\frac{{{x}^{2}}+2x+m}{x-2}\) có 2 điểm cực trị \(A,B\). Hãy tính k/c từ gốc tọa độ đến đường thẳng \(AB\)?

Cho CSC \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=2\) và số hạng thứ tư \({{u}_{4}}=17\). Công sai của cấp số cộng đã cho bằng?

Cho hình trụ có bán kính \(r=2\) và chiều cao \(h=3\). Diện tích xung quanh Sxq của hình trụ này bằng?

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

Cho \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức phân biệt của phương trình sau \({{z}^{2}}-4z+13=0\). Tính \({{\left| {{z}_{1}}+i \right|}^{2}}+{{\left| {{z}_{2}}+i \right|}^{2}}\)?

Trong không gian \(Oxyz\), cho điểm \(A\left( 1;1;-2 \right)\) và đt \(d:\frac{x-1}{2}=\frac{y+1}{1}=\frac{z}{-2}\). Đường thẳng qua \(A\) và song song với \(d\) có phương trình tham số là?

Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi các đồ thị sau \(y={{x}^{2}}-2x\), \(y=0\) trong mặt phẳng \(Oxy\). Quay hình \(\left( H \right)\) quanh trục hoành ta được một khối tròn xoay có thể tích bằng?

Trong không gian \(Oxyz\), cho \(A\left( 1;1;-2 \right)\); \(B\left( 2;0;3 \right)\); \(C\left( -2;4;1 \right)\). Mp đi qua \(A\) và vuông góc với đường thẳng \(BC\) có phương trình là?

Cho khối cầu có bán kính \(R=6\). Tính thể tích khối cầu bằng?

Cho HS \({y=x^{3}-3 m x^{2}+12 x+3 m-7}\) với \({m}\) là tham số. Số các giá trị nguyên của \({m}\) đề hàm số đã cho đồng biến trên \({\mathbb{R}}\) là?

Cho hàm số \(f\left( x \right)\) thỏa mãn \({f}'\left( x \right)={{x}^{2}}\left( x-1 \right),\forall x\in \mathbb{R}\). Phát biểu nào là đúng?

Cho HS \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:

Hàm số \(f\left( x \right)\) đồng biến trên khoảng nào dưới đây?

Cho hệ tọa độ \({O x y z}\), cho tam giác \({A B C}\) có \({A B=2 A C}\) và điểm \(M(2 ; 0 ; 4)\). Biết điểm \(B\) thuộc đường thẳng \(d: \frac{x}{1}=\frac{y}{1}=\frac{z}{1}\), điểm \(C\) thuộc mặt phẳng \((P): 2 x+y-z-2=0\) và \({A M}\) là phân giác trong của tam giác \({A B C}\) kẻ từ \(A(M \in B C)\). Phương trình đường thẳng \({B C}\) là?

Cho số phức \(z\) thỏa mãn \(\left| z+1 \right|\ge 1\). Gọi GTLN và GTNN của biểu thức \(P=\left| \frac{\left( 1+i \right)z+i+2}{z+1} \right|\) lần lượt là \(M\) và \(m\). Khi đó giá trị của \(\left( {{M}^{2}}+{{m}^{2}} \right)\) bằng?

Cho hàm số sau

\(f\left( x \right)=\left\{ \begin{align} & 3{{x}^{2}}\ln \left( x+1 \right)\text{ khi }x\ge 0 \\ & 2x\sqrt{{{x}^{2}}+3}+1\text{ khi }x<0 \\ \end{align} \right.\).

Biết \(\int\limits_{\frac{1}{e}}^{e}{\frac{f\left( \ln x \right)}{x}dx}=a\sqrt{3}+b\ln 2+c\) với \(a,b,c\in \mathbb{Q}\). Giá trị của \(a+b+6c\) bằng?

Trong không gian \(Oxyz,\) hình chiếu vuông góc của điểm \(M\left( 3;\,1;\,2 \right)\) lên trục \(Oy\) là điểm nào?