Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB=a, AD=2a\), SA vuông góc với mặt phẳng đáy và SA=a. Gọi M là trung điểm của AD. Tính khoảng cách giữa hai đường thẳng BM và SD
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai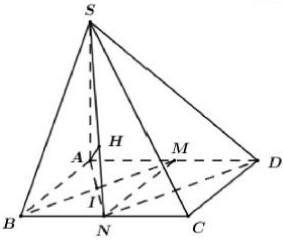
Gọi N là trung điểm của BC ta có:
\(\left\{ \begin{array}{l} DM = BN\\ DM//BN \end{array} \right. \Rightarrow \)DMBN là hình bình hành\( \Rightarrow BN//DM\)
\( \Rightarrow BM//\left( {SDN} \right) \supset SD \Rightarrow d\left( {BM;\left( {SDN} \right)} \right) = d\left( {M;\left( {SDN} \right)} \right)\)
Ta có \(\begin{array}{l} AM \cap \left( {SDN} \right) = D \Rightarrow \frac{{d\left( {M;\left( {SDN} \right)} \right)}}{{d\left( {A;\left( {SDN} \right)} \right)}} = \frac{{MD}}{{AD}} = \frac{1}{2}\\ \Rightarrow d\left( {M;\left( {SDN} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SDN} \right)} \right) \end{array}\)
Trong (ABCD) gọi I là trung điểm của BM
Ta có \(\left\{ \begin{array}{l} AM = BN\\ AM//BN \end{array} \right. \Rightarrow AMNB\) là hình bình hành, do đó hai đường chéo cắt nhau tại trung điểm mỗi đường nên I cũng là tủng điểm của AN, hay A,I,K thẳng hàng.
Xét tam giác AMB có AB=AM=a nên tam giác ABM vuông cân tại A\( \Rightarrow AI \bot BM \Rightarrow AN \bot DN\).
Ta có: \(\left\{ \begin{array}{l} DN \bot AN\\ DN \bot SA \end{array} \right. \Rightarrow DN \bot \left( {SAN} \right)\)
Trong (SAN) kẻ \(AH \bot SN\left( {H \in SN} \right)\) ta có: \(\left\{ \begin{array}{l} AH \bot SN\\ AH \bot DN \end{array} \right. \Rightarrow AH \bot \left( {SDN} \right) \Rightarrow d\left( {A;\left( {SDN} \right)} \right) = AH\)
Tam giác ABM vuông cân tại A \(\Rightarrow BM = a\sqrt 2 = AN\)
Áp dụng hệ thức lượng trong tam giác vuông SAN ta có:
\(AH = \frac{{SA.AN}}{{\sqrt {S{A^2} + A{N^2}} }} = \frac{{a\sqrt 6 }}{3}\)
Vậy \(d\left( {BM;SD} \right) = \frac{1}{2}AH = \frac{{a\sqrt 6 }}{6}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Khoa Học Tự Nhiên lần 3
Câu hỏi liên quan
-
Cho cấp số cộng \((u_n)\) có công sai d=2, \(u_1=-1\). Giá trị của \(u_5\) bằng
-
Đạo hàm của hàm số \(y=log_{2002}{(x^2+x)}\) là
-
Trong không gian Oxyz, mặt phẳng đi qua điểm M(0;-1;2) và song song với hai đường thẳng \({d_1}:\frac{{x + 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{z}{2},{d_2}:\frac{{x - 1}}{1} = \frac{y}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\) có phương trình là
-
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh \(a\sqrt2\). Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp đã cho
-
Đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 3}}\) có tất cả bao nhiêu đường tiệm cận
-
Gọi S là tập hợp các giá trị nguyên của m để mọi tiếp tuyến của đồ thị hàm số \(y=x^3-(m-1)x^2+(m-1)x+5\) đều có hệ số góc dương. Số phần tử của tập S là
-
Nghiệm của phương trình \(3^{x+2}=27\) là
-
Hàm số nào dưới đây có đồ thị như trong hình bên
-
Cho hàm số y = f (x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f (1- f (x)) = 2\) là:
-
Cho hàm số y=f(x) có đồ thị \(f'(x)\) như hình vẽ. Số điểm cực trị của hàm số y=f(x) là
-
Tập xác định của hàm số \(y = {\log _3}(x - 2)\) là
-
Cho hàm số y=f(x) có bảng xét dấu \(f'(x)\) như sau:
Hàm số \(y=f(2-3x)\) đồng biến trên khoảng nào dưới đây
-
Cho hàm số \(y={\sqrt{x-2}\over(x^2-4)(2x-7)}\). Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
-
Một lớp có 35 học sinh, số cách chọn ra 3 học sinh để tham gia văn nghệ trường là
-
Cho hàm số f(x) có bảng biến thiên
Số nghiệm của phương trình 2f(x)-3=0 là
-
Một công ty may mặc có hai hệ thống máy may chạy song song. Xác suất để hệ thống máy thứ nhất hoạt động tốt là 90%, hệ thống thứ hai hoạt động tốt là 85%. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy may hoạt động tốt. Xác suất để công ty hoàn thành đơn hàng đúng hạn là:
-
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình chữ nhật, \(AB=a, AD=a\sqrt2,\,SA\bot(ABCD) \,\mathrm{và}\,SA=a\), (tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng (SBD) bằng:
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M,N,P,Q,R,S lần lượt là tâm của các tâm của các mặt hình lập phương. Thể tích khối bát diện đều tạo bởi 6 đỉnh M,N,P,Q,R,S là
-
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=3, AD=4, AA'=5. Gọi O là tâm của đáy ABCD. Thê tích khối chóp O.A'B'C' bằng
-
Cho hàm số y=f(x) có đạo hàm \(f'(x)=(x^2-1)(x^2-3x+2)\). Số điểm cực trị của hàm số đã cho là
