Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AD=2\sqrt{2},\,\,AB=1,\,\,\)
\(SA=SB,\,\)\(SC=SD.\) Biết rằng hai mặt phẳng \(\left( SAB \right)\) và \(\left( SCD \right)\) vuông góc với nhau và tổng diện tích của hai tam giác \(SAB\) và \(SCD\) bằng \(\sqrt{3}.\) thể tích của khối chóp \(S.ABCD\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai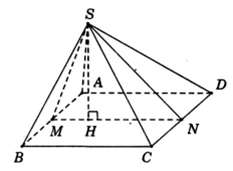
Gọi \(M,N\) lần lượt là trung điểm của \(AB,CD\)
Tam giác \(SAB\) cân tại \(S\) suy ra \(SM\bot AB\)
Vì \((SAB)\bot (SCD)\)suy ra \(SM\bot (SCD)\)
\(\Rightarrow SM\bot SN;(SMN)\bot (ABCD)\)
Kẻ \(SH\bot MN\)suy ra \(SH\bot (ABCD)\)
Ta có: \({{S}_{\Delta SAB}}+{{S}_{\Delta SCD}}=\sqrt{3}\)
\(\Leftrightarrow \frac{1}{2}.AB.SM+\frac{1}{2}.CD.SN=\sqrt{3}\)
\(\Rightarrow SM+SN=2\sqrt{3}\)
Tam giác \(SMN\) vuông tại \(S\)nên \(S{{M}^{2}}+S{{N}^{2}}=M{{N}^{2}}={{(2\sqrt{2})}^{2}}=8\)
Giải hệ
\(\left\{ \begin{matrix} SM+SN=2\sqrt{3} \\ S{{M}^{2}}+S{{N}^{2}}=8 \\ \end{matrix} \right.\)
\(\Leftrightarrow SM=1+\sqrt{3};SN=-1+\sqrt{3}\)
\(SH=\frac{SM.SN}{MN}=\frac{1}{\sqrt{2}}\)
Vậy thể tích khối chóp \({{V}_{SABCD}}=\frac{1}{3}.{{S}_{ABCD}}.SH=\frac{2}{3}\)
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Kiệm
Câu hỏi liên quan
-
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y=\ln x\), \(y=0\), \(x=1\), \(x=e\). Mệnh đề nào dưới đây đúng?
-
Cho \(f\left( 1 \right)=2\) và \(\int\limits_{1}^{3}{{f}'\left( x \right)dx}=6\) tính \(f\left( 3 \right)\)
-
Trong không gian \(Oxyz,\)cho mặt phẳng \(\left( P \right):2x-y+z-10=0\) và \(d:\frac{x+2}{2}=\frac{y-1}{1}=\frac{z-1}{-1}.\) Đường thẳng \(\Delta \) cắt \(\left( P \right)\) và đường thẳng \(d\) lần lượt tại \(M\)và \(N\) sao cho \(A\left( 1;3;2 \right)\)là trung điểm của \(MN.\) Tính độ dài đoạn thẳng \(MN.\)
-
Cho khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=2.\) Thể tích của khối chóp đã cho bằng
-
Trong hình vẽ dưới đây, điểm \(M\) là điểm biểu diễn của số phức nào?
.png)
-
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
-
Cho phương trình\({{z}^{2}}+az+2{{a}^{2}}=0\), với \(a\) là số thực dương. Gọi \({{z}_{1}},{{z}_{2}}\) là hai nghiệm phức của phương trình, trong đó \({{z}_{1}}\)có phần ảo dương. Biết rằng \(\left( 2{{z}_{1}}+{{z}_{2}} \right)\overline{{{z}_{1}}}=10+2\sqrt{7}i\). Khẳng định làm sau đây đúng?
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Số giá trị nguyên của tham số \(m\) để hàm số \(g\left( x \right)=f\left[ f\left( x \right)-m+1 \right]\) có đúng \(6\) điểm cực trị là
-
Tập nghiệm của bất phương trình \({{\log }_{3}}\left( x-2 \right)\le 2\) là
-
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm \(SD\) khi đó \(\sin \left( CM,\left( ABCD \right) \right)\) bằng
-
Cho ba điểm \(A\left( 1;2;-1 \right),\,\,B\left( 2;-1;3 \right),\,\,C\left( -3;5;1 \right).\) Tìm tọa độ điểm \(D\) sao cho \(ABCD\) là hình bình hành.
-
Một cấp số nhân gồm ba số hạng, biết số hạng thứ nhất và thứ hai lần lượt là \(-1;\,3.\) Số hạng cuối của cấp số nhân đó bằng
-
Cho mặt cầu có đường kính bằng \(8.\) Diện tích của mặt cầu đã cho bằng
-
Cho \(g\left( x \right)={{x}^{2}}-2x-1\) và hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Số nghiệm của phương trình \(f\left[ g\left( x \right) \right]=0\) là
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
Lấy ngẫu nhiên một số tự nhiên nhỏ hơn \(100,\) xác suất để lấy được một số chia hết cho \(6\) bằng
-
Số phức liên hợp của số phức \(z=-2+3i\) là
-
Có bao nhiêu giá trị nguyên \({b>1}\) để với mỗi giá trị của \({b}\) có đúng 5 số nguyên \(a\in \left( -10;10 \right)\) thỏa mãn \({\log _{3} \frac{2 a^{2}+3 a+b}{a^{2}-a+2} \leq a^{2}-6 a+7-b}\).
-
Cho hàm số \(y=f\left( x \right)\) có đồ thị \(y={f}'\left( x \right)\) cắt trục \(Ox\) tại ba điểm có hoành độ \(a,b,c\) như hình vẽ. Mệnh đề nào dưới đây đúng?
-
Cho hình hộp đứng có đáy là hình vuông cạnh bằng \(a,\) độ dài cạnh bên bằng \(3a.\) Thể tích của khối hộp đã cho bằng
